Перемещение объектов
Глава 6 Перемещение объектов
в макете
Устройства ввода

По своему опыту могу сказать, что при написании приложений для Microsoft Windows на пользовательский интерфейс обычно уходит больше времени, чем на все основное содержание программы. Думаю, при работе над любым продуктом хотя бы с удовлетворительным пользовательским интерфейсом на последний тратится около 75 процентов всего времени. Честно говоря, в своих приложениях я не вкладываю в него таких усилий (те читатели, которые имели несчастье с ними работать, в этом наверняка убедились).
Пожалуй, тщательнее всего я реализовываю интерфейс приложений, которые я пишу для своих детей. Они (приложения, а не дети) должны быть как можно проще. Например, однажды я написал для своего полуторагодовалого сына Марка простейший графический редактор, в котором пользовательский интерфейс почти полностью отсутствовал. В нем не было ни меню, ни кнопок, ни управляющих клавиш, и при работе с ним можно было даже обойтись без нажатия кнопок мыши. Тем не менее его инструменты позволяли нарисовать вполне нормальную картинку.
На прошлой неделе Марку исполнилось три года, и он начал проявлять интерес к ракетам, и потому я попробовал изобразить ракеты на своем компьютере. Приступая к работе над приложениями для этой книги, я обдумывал множество идей для игр, которые бы понравились Марку. Но вскоре стало очевидно, что клавиатура и мышь не могут обеспечить интерфейс для трехмерного приложения, который подошел бы трехлетнему ребенку. Честно говоря, мои первые эксперименты с перемещением трехмерных объектов не очень обрадовали даже меня самого. Проблема заключалась в том, что я пытался построить интерфейс на основе мыши и нескольких клавиш. Конечно, большинству читателей приходилось играть в трехмерные игры, которые имели вполне нормальный интерфейс на базе мыши и клавиатуры. Однако мой сын решительно не мог удерживать нажатой левую кнопку мыши вместе с клавишей Shift, да еще притопывать правой ногой от нетерпения.
На сцене появляется джойстик. Много лет назад, когда компьютеры приводились в действие энергией пара, а процессор 80286 казался чудом техники, я написал исходный драйвер джойстика для мультимедиа-расширения Microsoft Windows (кстати говоря, довольно сомнительная заслуга). Впрочем, все это было давно, и с тех пор я прочно забыл о существовании джойстиков, пока несколько недель назад не зашел в магазин Microsoft. Именно в этот момент я решил, что мои трехмерные приложения будут работать под управлением джойстика, и купил
/b> ¦¦ у Глава 6. Перемещение объектов в макете
Microsoft SideWinder Pro. Довольно быстро выяснилось, что в трехмерных приложениях джойстик действительно удобнее мыши. SideWinder обладает четырьмя параметрами, генерирующими данные для приложения: координатами Х и Y, угловой и линейной скоростью. С помощью кнопок на боковой поверхности джойстика я мог вращать объект вокруг трех осей и управлять его положением.
Немного позднее мне подарили манипулятор SpaceBall Avenger — весьма эффектное устройство, выпущенное компанией Spacetec IMC Corp. Он обладает шестью степенями свободы, то есть позволяет получить выходные параметры для смещения по осям х, у и z, а также для вращательного движения вокруг осей r, u и v. В конструкции манипулятора использованы датчики давления, которые с высокой чувствительностью реагируют на все толчки и повороты шарика.
Итак, у меня появились два джойстика, которые работали по-разному, а программа поддерживала только один из них. Я решил создать обобщенную модель устройства ввода, которую можно было бы приспособить к любому конкретному устройству и настроить его так, как мне хочется. Поначалу казалось, что задача не из сложных — во всяком случае, до тех пор, пока я не взялся за нее. Результат моих стараний не назовешь шедевром, однако он вполне пригоден для практического использования — если у вас есть 10—15 свободных минут, вы сможете настроить свой джойстик самым немыслимым образом. После того как работа была завершена, я подумал, что она по крайней мере послужит примером того, как можно построить обобщенную модель устройства ввода. Я бы не советовал распространять ее в коммерческих целях, если вы дорожите своей репутацией.
Время, потраченное на настройку джойстика, вознаграждается сторицей: мой сын обожает гонять объекты по экрану, выкручивая рукоять джойстика или беспорядочно толкая SpaceBall во всех направлениях.
Для полноценной работы с приложением из этой и последующих глав я бы порекомендовал купить джойстик — общаться с ним гораздо удобнее, чем с мышью.
Модель устройства ввода
На Рисунок 6- 1 изображена модель устройства ввода* с точки зрения приложения. Когда приложению требуется выполнить цикл обновления, оно вызывает функцию Update объекта, управляющего процессом ввода (контроллера ввода). Контроллер опрашивает устройство ввода и получает обновленную информацию о его аппаратном состоянии. Узнав ее, контроллер изменяет положение и ориентацию фрейма, к которому он присоединен в приложении, а затем уведомляет приложение о причине обновления состояния. Все эти действия обычно совершаются в периоды пассивности приложения. Помимо событий, изображенных на Рисунок 6-1, возможны и другие. В частности, любые сообщения от клавиатуры или мыши, полученные окном, в котором воспроизводится трехмерное изображение, передаются контроллеру и устройству ввода. Это делается для того, чтобы получать входные данные от мыши или клавиатуры без обязательного опроса этих устройств.
• Обратите внимание на то, чти устройством ввода (input device) в данном случае автор называет не физическое устройство (клавиатура, мышь, джойстик), а класс C++, назначением которого является генерация входных данных для программы. — Примеч. персе.
Модель устройства ввода ^Щ' 135
Рисунок. 6-1. Рабочий цикл устройства ввода

Устройство ввода
Назначение устройства ввода состоит в том, чтобы получить данные от аппаратуры и сгенерировать по ним шесть величин: х, у, z, r, u и v. Значения х, у и z представляют собой линейные смещения, а r, u и v — угловые скорости. Оси устройства ввода не связаны с осями макета или конкретного объекта; это не более чем необработанные входные данные, которые используются контроллером для смены положения объекта. На Рисунок 6-2 показаны общие зависимости между осями и угловыми скоростями.
Разумеется, при работе с таким устройством, как SpaceBall, значения х, у, z, г, u и v генерируются просто — достаточно опросить аппаратуру, применить некоторый масштабный множитель и вернуть результат. Для физических устройств, не способных генерировать данные по шести осям, устройство ввода должно получить аппаратные данные и обработать их так, чтобы создать выходные значения для всех шести параметров. Например, устройство ввода из библиотеки 3dPlus, работающее с мышью, получает координаты х и у курсора мыши и в зависимости от состояния клавиш Shift и Ctrl определяет, какие выходные значения следует изменить. Таким образом, если во время перемещения мыши удерживать левую кнопку и не нажимать никаких клавиш, изменяются координаты х и у. При нажатой клавише Shift входное значение координаты х переходит в угловую скорость v, а координата у—в координату z.
/b>
Глава 6. Перемещение объектов в макете
Рисунок. 6-2. Взаимосвязь между значениями r, u, v и х, у, z

Библиотека 3dPlus включает поддержку трех различных устройств ввода: клавиатуры, мыши и джойстика. Каждое устройство реализовано в виде класса C++, производного от C3dlnputDevice.
Устройство ввода с клавиатуры
Устройство ввода с клавиатуры обрабатывает сообщения WM_KEYDOWN, посылаемые ему контроллером. Сообщения клавиатуры используются для увеличения или уменьшения текущих значений параметров x,y,z,r,unv.B табл. 6-1 показано, как различные комбинации клавиш влияют на значения выходных параметров.
| Таблица 6-1. Управляющие функции клавиатуры | |||
| Клавиша | Normal | Shift | Ctrl |
| Left arrow | X- | V- | u- |
| Right arrow | X++ | V++ | U++ |
| Up arrow | Y++ | Z++ | R++ |
| Down arrow | Y- | z- | R- |
| Знак «+» на цифровой клавиатуре | Z- | ||
| Знак «-» на цифровой клавиатуре | Z++ | ||
| Page Up | V++ | ||
| Page Down | V- | ||
| Home | U++ | ||
| End | u- | ||
| Insert | R++ | ||
| Delete | R- |
Функция, управляющая работой устройства ввода с клавиатуры, представляет собой оператор switch, в котором обрабатываются сообщения от различных клавиш. Ниже приведена первая часть функции из файла SdlnpDev.cpp каталога Source библиотеки 3dPlus, обрабатывающая нажатия клавиш <— и —>:
void C3dKeyInDev::OnKeyDown(HINT nChar, UINT nRepCnt,
UINT nFlags)
(
double dine = 0.02;
switch (nChar) { case VKJ3HIFT:
in_bShift = TROE;
break;
case VK_CONTROL:
m_bControl = TRUE;
break;
case VK_RIGHT:
if (m_b3hift) { Inc(m_st.dV) ;
} else if (m_bControl) { Inc(m_st.dU) ;
) else (
Inc(m_st.dX) ;
} break;
case VK_LEFT:
if (m_bShift) { Dec(m_st.dV) ;
} else if (m_bControl) { Dec(m_st.dU) ;
) else (
Dec(m_st.dX) ;
} break;
Устройство ввода от мыши
Устройство ввода от мыши выглядит несколько проще. Поскольку мышь обладает только двумя степенями свободы, необходимо определить, каким образом два входных параметра отображаются на шесть выходных осей (табл. 6-2).
Таблица 6-2. Управляющие функции мыши
Входной параметр Normal Shift Ctrl
X X -V -U
Y -Y -Z -R
/b> iiisi^ Глава б. Пепемешение объектов в макете
Обратите внимание на то, что некоторые параметры инвертируются. Я изменил направление осей, чтобы управление стало более логичным. Код устройства ввода от мыши состоит из двух функций: C3dMouselnDev::OnUserEvent и C3dMouselnDev::GetState. Первая функция, исходный текст которой приведен ниже, находится в файле 3dlnpDev.cpp. Данная функция обрабатывает перемещение мыши и захватывает ее указатель (то есть ограничивает его перемещение текущим окном) при нажатии левой кнопки:
void C3dMouseInDev::OnUserEvent(HWND hWnd, UINT uiMsg,
WPARAM wParam, LPARAM IParam) (
switch (uiMsg) { case WM_LBUTTONDOWN:
::SetCapture(hWnd) ;
m_bCaptured = TRUE;
break;
case WM_LBUTTONUP:
if (m_bCaptured) { ::ReleaseCapture () ;
m_bCaptured = FALSE;
} break;
case WM_MOUSEMOVE:
if (m_bCaptured) (
// Внимание: экранные координаты! (см. C3dWnd)
m_ptCur.x = LOWORD(IParam);
m_ptCur.y = HIWORD(IParam);
m_dwFlags = wParam;
} break;
default:
break;
}
\ i
Положение мыши запоминается в m_ptCur, локальной структуре класса CPoint. Вторая функция, исходный текст которой приведен ниже, вызывается, когда контроллер запрашивает текущее состояние устройства ввода:
BOOL C3dMouseInDev::GetState(_3DINPUTSTATE& st) {
if (m_ptPrev.x « 0) { m_ptPrev = m_ptCur;
}
Устоойство ввода '"SH 139
if (m_dwFlags & MK_SHIFT) {
m_st.dz = -d;
} else if (m_dwFlags & MK_CONTROL) {
rri_st.dR = -d;
} else (
m_st.dY = -d;
) )
m_ptPrev = m_ptCur;
st = m_st;
return TRUE;
Функция обрабатывает полученные значения х и у таким образом, чтобы обеспечить небольшую «мертвую зону» для малых смещений и предотвратить случайное перемещение объекта. Затем смещения умножаются на коэффициент пропорциональности, чтобы перемещение объектов всегда происходило в правильном масштабе. Наконец, в зависимости от текущего состояния клавиш Shift и Ctrl функция определяет, какие выходные параметры следует изменить.
Устройство ввода от джойстика
Устройство ввода от джойстика реализуется несколько сложнее, чем ввод от мыши или клавиатуры. На Рисунок 6-3 изображено окно диалога Joystick Settings.
Рисунок. 6-3. Окно диалога Joystick Settings

Значение каждого выходного параметра может определяться по любой из входных осей, а кнопка джойстика может выступать в роли модификатора. Например, из Рисунок 6-3 видно, что значение выходного параметра v определяется значением входного параметра х, но только при нажатой кнопке 4. В столбцах Value изображены текущие значения параметров. Левый столбец показывает те-
Угтплмгтял капля
141
кущее входное значение, полученное от джойстика; темно-серая полоса соответствует «мертвой зоне». Если входное значение лежит внутри «мертвой зоны», выходное значение не изменяется. Наличие «мертвой зоны» позволяет предотвратить мелкие смещения объектов в тех случаях, когда отпущенная рукоять джойстика не возвращается точно к нейтральному положению. Правый столбец Value изображает выходное значение параметра.
Кроме того, вы можете изменить масштабы осей. Увеличение числа в столбце Scale соответствует повышению чувствительности джойстика, причем отрицательные значения меняют направление оси на противоположное. Конфигурация, показанная на рисунке, была выбрана мной для джойстика Microsoft SideWinder. При работе со SpaceBall остается лишь задать коэффициент пропорциональности между параметрами (х отображается на х, у — на у и т. д.). На Рисунок 6-4 изображен типичный график зависимости выходных значений параметров от входных. Плоский участок в центре соответствует «мертвой зоне».
Рисунок* 6-4» Типичный график зависимости вход/выход для джойстика

Конфигурация джойстика сохраняется в системном реестре. Я решил создавать отдельный вариант конфигурации для каждого типа джойстика и для каждого приложения. Если у вас имеются несколько джойстиков, то при смене активного джойстика можно обойтись без повторной конфигурации. Не исключено, что идея сохранения отдельной конфигурации для каждого приложения покажется довольно странной, но я обнаружил, что в некоторых приложениях желательно настроить джойстик нестандартным образом. Данные конфигурации хранятся в реестре с ключом:
HKEY_CURRENT_USER\Software\3dPlus\<<MMH-npKnoiKeHMA>>\Sett.i.i-igs \Joystick\«тип-джойстика»
Большой объем кода для работы с джойстиком не позволяет привести его в книге, поэтому я предлагаю вам просмотреть файл 3dJoyDev.cpp в каталоге Source библиотеки 3dPlus.
Гпаоа R Попоклашаииа /^Дт-ои-г^о о идилата
Контроллер ввода
Задача контроллера ввода заключается в том, чтобы получить от устройства ввода значения параметров х, у, z, r, u и v и определенным образом применить их к объекту CSdFrame. Я создал два различных типа контроллеров ввода: позиционный контроллер (position controller) и контроллер полета (flying controller). Контроллеры обоих типов могут использоваться для манипуляций с объектами макета или с камерой. Контроллеру необходимо указать фрейм, с которым он должен работать, а остальное происходит автоматически. Помимо перемещения объекта, контроллер уведомляет приложение о различных событиях — скажем, об изменении параметра х или о нажатии определенной кнопки, — на которые приложение должно реагировать определенным образом. На Рисунок 6-5 изображено окно диалога, которое вызывается из меню Edit приложения Moving. Здесь можно выбрать разновидность контролируемого объекта, тип контроллера и устройство ввода.
Рисунок. 6-5. Окно диалога Control Device

Позиционный контроллер используется для перемещения объектов внутри макета. Параметры х, у и z определяют положение объекта по отношению к фрейму макета; следовательно, при смещении джойстика влево объект перемещается вдоль оси х макета. Повороты происходят относительно оси объекта, а не начала координат, и это выглядит достаточно разумно. Например, при повороте джойстика объект вращается, а его центр тяжести остается на месте. Любой пользователь может достаточно быстро научиться работать с таким контроллером и перемещать объекты внутри макета.
Позиционный контроллер также может использоваться для перемещения камеры, что, в сущности, равносильно перемещению всего макета. Тем не менее результаты такого перемещения иногда выглядят довольно странно, поскольку все движения осуществляются по отношению к макету, а не к камере; если развернуть камеру вокруг оси у на 90 градусов, чтобы она была обращена влево, любое движение вперед будет восприниматься как движение вправо.
Контроллер полета используется для имитации «полета» объекта или камеры внутри макета. Параметры х и у служат для определения углов атаки и крена,
z определяет скорость, а и — угол тонгажа. Идея состоит в том, чтобы привести объект в прямолинейное движение и затем выбирать его траекторию посредством изменения углов атаки, крена и тонгажа. В исходном варианте программы углы крена и атаки умножались на скорость, чтобы имитация получалась более реалистичной. Однако вскоре выяснилось, что пилота из меня не выйдет, поэтому я пошел по более простому пути и допустил изменение ориентации даже для неподвижного объекта. Если вам это покажется нелогичным, попробуйте поработать с текущим вариантом и затем модифицировать его так, чтобы учитывать скорость полета. Что же именно модифицировать, спросите вы? Приведенную ниже функцию, которая находится в файле 3dlnCtlr:
void C3dFlyCtlr::OnUpdate(_3DINPUTSTATE& st,
C3dFrame* pFrame) t
// Определить скорость (по значению параметра z)
double v = st.dZ / 10;
// Получить углы атаки, крена и тонгажа // для осей х, у и и double pitch = st.dY / 3;
double roll = -st.dX / 3;
double yaw = 5t.dU / 5;
// Умножить угол атаки и крена на скорость // для повышения реализма // pitch *= v;
// roll *= v;
pFrame-»AddRotation(l, 0, 0, pitch, D3DRMCOMBINE_BEFORE) ;
pFrame-»AddRotation(0, 0, 1, roll, D3DRMCOMBINE BEFORE);
pPrame-»AddRotation(0, 1, 0, yaw, D3DRMCOMBINE^BEFORE) ;
// Получить вектор текущего направления double xl, yl, zl;
pFrame-»GetDirection (xl, -yl, zl);
// Умножить вектор направления на скорость xl *= v;
yl *= v;
zl *= v;
// Определить текущее положение double х, у, z;
pFrame-»GetPosition (х, у, z);
// Обновить текущее положение х += xl;
У += yl;
z += zl;
/b> ^Р? Глава 6. Перемещение объектов в макете
pFrame-»SetPosition (x, y, z
Функция C3dFlyCtrl::OnUpdate изменяет положение и ориентацию фрейма перемещаемого объекта на основании данных, полученных от устройства ввода. Эта функция вызывается каждый раз, когда требуется обновить положение объекта. Ее аргументами являются описание текущего состояния входного устройства (значения его параметров) и указатель на фрейм, с которым она должна работать. Из всего кода контроллеров и устройств ввода данная функция представляет наибольший интерес, поэтому мы подробно рассмотрим ее.
Начнем со структуры для хранения данных, полученных от джойстика:
typedef struct 3DINPUTSTATE {
double dX // -1«= значение «=1
double dY // -1«= значение «=1
double dZ // -1«= значение «=1
double dR // -1«= значение «=1
double dU // -1«= значение «=1
double dV // -1«= значение «=1
double dpov; // 0 «= значение «=359
// (значения «О являются недопустимыми) DWORD dwButtons;// I = кнопка активна (нажата) ) _3DINPUTSTATE;
Как видно из листинга, значения шести основных параметров лежат в интервале от -1,0 до 1,0. Кроме того, в структуре присутствует член dPov, определяющий направление, в котором вы смотрите, — вперед, влево, вправо и т. д. (на некоторых джойстиках имеется специальная кнопка для выбора направления). Значение dPov представляет собой угол в градусах, измеряемый от направления «вперед».
Контроллер задает скорость и углы крена, атаки и тонгажа по входным значениям параметров z, x, у и и соответственно. Для повышения чувствительности я применил масштабные коэффициенты, значения которых были определены эмпирическим путем.
Если вы захотите усложнить управление летящим объектом, попробуйте убрать комментарии из строк, в которых углы атаки и крена умножаются на скорость.
После определения текущей скорости и величины смещения объекта, следующим шагом является применение поворотов к фрейму. Для этого мы вызываем функцию AddRotation и указываем, что поворот должен быть выполнен до текущего преобразования. Это необходимо для того, чтобы объект вращался вокруг собственной оси, а не вокруг оси макета.
Завершающий шаг — перемещение объекта в новое положение. Сначала мы вызываем функцию GetDirection, чтобы получить вектор направления объекта (то есть направление, в котором он летит). Затем вектор направления умножается на скорость — их произведение равно величине смещения от текущего положения объекта. Наконец, мы определяем текущее положение объекта, прибавляем к нему смещение и переносим объект в новое положение.
Возможно, вы обратили внимание на то, что в программе используются версии функций GetDirection, GetPosition и SetPosition, в которых значения x, у и z
Устройство ввода
/h2>
заданы в виде отдельных аргументов, а не в виде объекта C3dVector. Никакой особой причины для этого нет, и вы вполне можете в качестве упражнения переписать данные функции с использованием аргументов-векторов.
Последнее замечание: скорость перемещения в нашем случае не является постоянной. Функции обновления вызываются в периоды пассивной работы приложения, а количество времени, которое требуется для перерисовки макета, зависит от взаимного расположения объектов. Если вы захотите добиться постоянной скорости перемещения, придется пойти более сложным путем — например, измерять текущее время функцией timeGetTime (объявленной в файле Mmsystem.h) и определять смещение каждого объекта в зависимости от времени.
Самостоятельно движущиеся объекты
Контроллер полета способен привести объект в движение, однако все равно вам приходится непрерывно управлять его перемещением. Лично я не люблю подолгу сидеть за рулем, поэтому разработал несколько примеров того, как заставить объекты самостоятельно двигаться по фиксированной траектории.
Первый пример, находящийся в каталоге Cruise, приводит в движение камеру, чтобы создать иллюзию кругового полета на самолете вокруг горы. На Рисунок 6-6 изображен внешний вид экрана приложения (кроме того, на вкладке имеется цветная иллюстрация).
Рисунок. 6-6. Полет над холмами

Перед тем как писать это приложение, я нарисовал план местности на миллиметровке, обозначив на нем границы всех холмов. Затем я вручную закодировал все вершины и данные граней для создания ландшафта. Не стану приводить здесь фрагмент исходного текста, поскольку он состоит лишь из длинного массива вершин, за которыми следует не менее длинный список данных граней. При желании можете найти его в файле MainFrm.cpp в каталоге Cruise.
/h2>
Глава 6. Перемещение объектов в макете
Кроме того, я вручную изобразил небольшой самолет и наложил на ландшафт текстуру, чтобы придать ему более привлекательный вид (создание и применение текстур рассмотрено в главе 8). Последним этапом в создании макета стала установка камеры в начальной позиции и увеличение ее обзорного поля для получения более широкой панорамы:
BOOL CMainFrame::SetScene() t
// Задать траекторию полета камеры m_vCamera = C3dVector(5, 5, 0);
m_dRadius = 5.0;
// Задать обзорное поле m_pScene-»SetCameraField (1.5) ;
}
Траектория выбирается таким образом, чтобы камера вращалась вокруг заданной точки. На Рисунок 6-7 изображено движение камеры в нашем макете.
Рисунок. 6-7. Траектория полета камеры

Все, что осталось сделать, — организовать совместное перемещение камеры и самолета при каждой итерации:
BOOL CMainFrame::Update(double d)
(
// Обновить положение камеры C3dMatrix r;
r.Rotate(0, 2.0, 0) ;
m vCamera = r * m vCamera;
m_pScene-»SetCameraPosition (m_vCamera) ;
// Задать верхний вектор C3dVector vu(0, 1, 0) ;
// Построить вектор направления C3dVector vf = m_vCamera * vu;
m_p3cene-»SetCameraDirection (vf, vu) ;
// Задать положение самолета относительно камеры r.Rotate(0, 20, 0);
C3dVector vp = r * m vCamera;
m_pPlane-»SetPosition(vp) ;
// Задать направление C3dMatrix rp;
rp.Rotate(0, 0, 10); // Слегка покачаем крьшьями vu = rp * vu;
vf = vp * vu;
m_pPlane-»SetDirection (vf, vu) ;
return m_wnd3d.Update(TRUE);
)
Текущее положение камеры хранится в объекте C3dVector. Для определения ее нового положения вектор умножается на матрицу поворота. Затем камера переносится на новое место — но это еще не все. Необходимо изменить ориентацию камеры, чтобы она по-прежнему была направлена по касательной к окружности. Чтобы вычислить новое направление камеры, мы умножаем (векторно) верхний вектор (vu) на вектор положения камеры (m_vCamera). Вектор-результат совпадает с вектором направления камеры (Рисунок 6-8).
Вычисление вектора направления камеры 148 SUSy Глава 6. Пеоемешение объеет-ов в мякртр

Векторное произведение оказывается очень полезным, когда требуется найти вектор, перпендикулярный плоскости, которая определена двумя другими векторами, как в нашем случае.
Последнее, что осталось сделать, — вычислить положение и направление маленького самолета, летящего перед камерой. Самолет перемещается по той же траектории, что и камера, однако он на несколько градусов опережает камеру. Чтобы определить положение самолета, мы берем вектор положения камеры и поворачиваем его чуть дальше, пользуясь для этого другой матрицей (г). При определении ориентации самолета я сначала вычислял векторное произведение точно так же, как и для камеры. Однако мне показалось, что смотреть на самолет, который идеально ровно летит впереди камеры, довольно скучно. Я слегка повернул вектор вверх, чтобы создать иллюзию покачивания самолета. Эффект не очень впечатляющий, но зато легко реализуемый.
Относительное движение
Наше следующее приложение имитирует часовой механизм, состоящий из нескольких частей, которые находятся в непрерывном движении по отношению друг к другу. На Рисунок 6-9 изображен внешний вид окна приложения, находящегося в каталоге Clock (на вкладке имеется цветная иллюстрация).
Рисунок. 6-9. Часовой механизм

Механизм состоит из трех вращающихся стержней. К центральному стержню прикреплена минутная стрелка и небольшая шестеренка. Ко второму стержню, охватывающему часть центрального, прикреплена часовая стрелка и большая шестеренка. На третьем стержне имеются две шестеренки, большая и маленькая, которые сцеплены с шестеренками для двух стрелок — минутной (центральный стержень) и часовой (внешний стержень).
/h2>
Относительное движение
Когда я впервые попытался создать это приложение, то изобразил шестеренки в виде дисков, и на «все про все» у меня ушло около часа. Отладка работы шестеренок потребовала уже целых трех часов! Фрагмент кода, в котором конструируется данный механизм, выглядит довольно просто. Сначала мы создаем стержни и присоединяем к ним шестеренки и стрелки в качестве фреймов-потомков. Затем начинаем вращать стержни. Я подобрал частоту вращения таким образом, чтобы создать впечатление, будто механизм действительно приводится в действие шестеренками. Если внимательно присмотреться, можно заметить, что иллюзия получилась не полной.
Чтобы весь часовой механизм вращался в окне, я создал фрейм, являющийся родительским по отношению ко всем трем стержням. Когда этот фрейм поворачивается вокруг оси у, изображение работающего механизма также начинает вращаться (наблюдательные читатели могли заметить, что передаточный коэффициент шестеренок составляет 4:1 вместо более привычного 12:1, как в большинстве часов). Давайте рассмотрим фрагмент файла MainFrm.cpp, в котором создается стержень с минутной стрелкой. Два других стержня определяются аналогичным образом:
BOOL CMainFrame::SetScene() (
// Создать часовой механизм C3dFrame clock;
clock.Create(m_pScene) ;
double dSpin = -0.1;
// Создать стержень с минутной стрелкой C3dFrame si;
si.Create(Sclock) ;
C3dShape rl;
rl.CreateRod(0, 0, -0.5, О, О, 10, 0.4, 16);
rl.SetColor(0, 0, 1);
sl.AddChild(Srl) ;
// Присоединить минутную стрелку CHand bighand(lO) ;
sl.AddChild(Sbighand) ;
bighand.SetPosition(0, 0, 0) ;
// Присоединить шестеренку CGear gl(1.5, 1.5, 8) ;
sl.AddChildf&gl) ;
gl.SetPosition(0, 0, 5.5);
// Привести стержень во вращение sl.SetRotation(0, 0, 1, dSpin);
}
/b> Я»:'?' Глава 6. Перемещение объектов в макете
Фрейм стержня создается как потомок по отношению к фрейму всего механизма. Затем к фрейму стержня присоединяется цилиндрический объект, который является его визуальным представлением. Минутная стрелка создается как объект класса CHand, производного от CSdShape, который мы рассмотрим чуть позже. Шестеренка тоже является объектом отдельного класса CGear, производного от CSdShape, и точно так же присоединяется к фрейму стержня. Последнее, что осталось сделать, — привести фрейм во вращение функцией C3dFrame::SetRotation.
Стрелки создаются из двух цилиндров и конуса:
CHand::CHand(double 1)
{
CreateRod(0, 0, О, О, О, 0.5, 1, 16);
SetColor(l, 1, 0);
CSdShape r;
r.CreateRod(0, 0, 0.25, 0, 1-3, 0.25, 0.20, 16);
r.SetColor(0, 0, 1);
AddChild(&r) ;
CSdShape с;
c.CreateCone(0, 1-3, 0.25, 0.75, TRUE, 0, 1, 0.25, 0, FALSE, 16);
c.SetColor(l, 1, 0);
AddChild(Sc) ;
}
С шестеренками дело обстоит несколько сложнее. Внешний и внутренний радиус зубцов определяется двумя окружностями. Затем окружности разбиваются на части по числу зубцов, что и дает нам положения вершин (Рисунок 6-10). Генерация списка данных для внешних граней зубцов завершает первую стадию создания фигуры.
Рисунок. 6-10. Конструирование зубцов шестеренки

При создании боковых граней шестеренки используются нормали, чтобы грани воспроизводились в виде плоских поверхностей. Если не задавать нормали, механизм визуализации скругляет стороны шестеренок, и на их гранях появляют-
Относитепьное лвижймий Ш^ 151
ся какие- то странные треугольные ячейки. Разумеется, за пять минут работы с Autodesk 3D Studio можно было бы создать идеальные шестеренки и без этого кода:
CGear::CGear(double r, double t, int teeth)
{
double twopi = 6.28318530718;
double rl = r - 0.3;
double r2 = r + 0.3;
int nFaceVert = teeth * 4;
int nVert = nFaceVert * 2;
D3DVECTOR* Vertices = new D3DVECTOR[nVert];
D3DVECTOR* pv = Vertices;
double da = twopi / (teeth * 4);
double a = 0;
for (int i = 0; i « teeth; i++) {
pv-»x = rl * cos(a);
pv-»y = rl * sin(a);
pv-»z = 0;
pv++;
a += da ;
pv-»x = r2 * cos (a) ;
pv-»y = r2 * sin(a);
pv-»z = 0;
pv++;
a += da;
pv-»x = r2 * cos(a);
pv-»y = r2 * sin(a);
pv-»z = 0;
pv++;
a += da;
pv-»x = rl * cos(a);
pv-»y = rl * sin(a);
pv-»z = 0;
pv++ ;
a += da;
}
pv = Vertices;
D3DVECTOR* pv2 = SVertices[nFaceVert] ;
for (i = 0; i « nFaceVert; i++) {
*pv2 = *pv;
pv2-»z = t;
pv++;
pv2++;
}
// Сгенерировать данные граней для зубцов.
// Нервных просят не смотреть!
int nf = (teeth * 5 * 4) + (teeth * 26) + 10;
/b>
Глава 6. Перемещение объектов в макете
int* FaceData = new int[nf] ;
int* pfd = FaceData;
for (i = 0; i « teeth*4; i++) {
*pfd++ = 4;
*pfd++ = i;
*pfd++ = (i + 1) % (teeth*4);
*pfd++ = nFaceVert + ((i + 1) % (teeth*4));
*pfd++ = nFaceVert + (i % (teeth*4));
}
// Завершить список *pfd++ = 0;
Create(Vertices, nVert, NULL, 0, FaceData, TRUE);
// Добавить торцевые грани с заданием нормалей D3DVECTOR nvect [] = {
(О, 0, 1},
(О, 0, -1} };
delete [] FaceData;
FaceData = new int [teeth * 9 + teeth * 4 + 10] ;
pfd = FaceData;
for (1=0; i « teeth; i++) {
*pfd++ = 4;
*pfd++ = i*4;
*pfd++ = 1;
*pfd++ = i*4+3;
*pfd++ = 1;
*pfd++ = i*4+2;
*pfd++ = 1;
*pfd++ = i*4+l;
*pfd++ = 1;
}
*pfd++ = teeth*2;
for (i = teeth-1; i »= 0; i-) {
*pfd++ = i*4+3;
*pfd++ = 1;
*pfd++ = i*4;
*pfd++ = 1;
}
*pfd++ = 0;
AddFaces(Vertices, nVert, nvect, 2, FaceData);
pfd = FaceData;
for (i = 0; i « teeth; i++) {
*pfd++ = 4;
Относительное движение тЩ!) 153
*pfd++ = nFaceVert + i*4;
*pfd++ = 0;
*pfd++ = nFaceVert + i*4+l;
*pfd++ = 0;
*pfd++ = nFaceVert + i*4+2;
*pfd++ = 0;
*pfd++ = nFaceVert + i*4+3;
*pfd++ = 0;
}
*pfd++ = teeth*2;
for (i = 0; i « teeth; i++) {
*pfd++ = nFaceVert + i*4;
*pfd++ = 0;
*pfd++ = nFaceVert + i*4+3;
*pfd++ = 0;
}
*pfd = 0;
AddFaces(Vertices, nVert, nvect, 2, FaceData);
delete [] Vertices;
delete [] FaceData;
SetColor(l, 1, 0);
}
К пастоящему моменту весь этот фрагмент должен казаться вам вполне понятным. Когда у меня будет немного свободного времени, я непременно сделаю на основе данного приложения настоящие часы с секундной, минутной и часовой стрелками, с циферблатом и маятником.
Перемещение объектов по произвольным траекториям
Конечно, объект можно перемещать по любой траектории. Для этого необходимо задать либо набор координат в пространстве, либо функцию (например, генератор сплайнов), которая строит плавную кривую для траектории, описанной несколькими точками. При каждой новой итерации вы определяете новое положение объекта и перемещаете его туда. Не забывайте, что вам также придется вычислять вектор направления объекта и, возможно, его верхний вектор (если только перемещаемый объект не является сферой).
Создание собственного контроллера движения
Перемещение объектов и полеты — это, конечно, хорошо, но что делать, если вам понадобится что-то другое? Давайте посмотрим, как создать контроллер движения для более интересного объекта — космического танка Mark VII с доплеров-ским радаром Х-диапаэона. Танк может передвигаться по поверхности планеты с различной скоростью и поворачивать на ходу. Его башня быстро вращается, а пушка
/b> в!^' Глава 6. Перемещение объектов в макете
поднимается. Кажется, я забыл упомянуть о радаре, который радостно вертится на башне? На Рисунок 6-11 изображен танк Mark VII при выполнении боевого задания.
Рисунок. 6'П. Космический танк Mark VII с доплеровским радаром Х-диапазона

Хмм... вы обратили внимание на то, что у танка нет колес? Могу предложить два объяснения:
• Это летающий танк.
• Мне было лень возиться с колесами.
Решайте сами.
На Рисунок 6- 12 изображена диаграмма подвижных частей танка (вместе с колесами). Иллюстрация приведена на цветной вкладке.
. Составные части танка

Создание собственного контроллера движения
/h2>
В приложении Tank класс C3dTank является производным от C3dFrame. Последовательность, в которой строится танк, такова: сначала мы присоединяем корпус к внешнему фрейму, затем присоединяем башню к корпусу и в последнюю очередь присоединяем пушку и радар к башне. Радар приводится в постоянное вращение. Пушка может подниматься и опускаться, вращаясь вокруг своей горизонтальной оси. Башня может вращаться вокруг вертикальной оси корпуса.
Перед тем как заниматься контроллером, давайте рассмотрим фрагмент кода, в котором создается танк, чтобы нам было легче управлять им:
C3dTank::C3dTank() {
// Создать фрейм
C3dFrame::Create(NULL) ;
// Загрузить составные части танка и построить танк
m_hull.Load(IDX_HULL) ;
AddChild(&m_hull) ;
m_turret.Load(IDX_TURRET) ;
m hull.AddChild(&m_turret);
m_gun.Load(IDX_GUN) ;
m_turret.AddChild(&m_gun) ;
// Радар имеет собственный фрейм,
// чтобы было удобнее управлять осью вращения
C3dFrame rframe;
rframe.Create(&m_turret);
C3dShape radar;
radar.Load(IDX_RADAR) ;
rframe.AddChild(Sradar) ;
radar.SetPosition(0, 0, -0.3);
rframe.SetPosition(О, О, 0.3);
rframe.SetRotation(0, 1, 0, 0.1);
SetGun(25) ;
}
Единственное, что может здесь показаться странным, — это то, что я использовал для радара отдельный фрейм. Мне пришлось поступить так из-за того, что в первоначальном варианте танка ось у радара была смещена относительно того места, где я хотел расположить радар. Поэтому я задал начало координат фрейма в той точке башни, где помещается ось, и сместил объект-радар внутри фрейма, чтобы он находился над осью вращения (Рисунок 6-13).
Все объекты, из которых состоит наш танк, были созданы в 3D Studio и преобразованы в формат .X с помощью утилиты conv3ds, входящей в DirectX 2 SDK. Они были включены в файл приложения RC2 в качестве ресурсов:
//
// STAGE.RC2 - resources Microsoft Visual C++ does not edit
directly
//
/b> fy Глава 6. Перемещение объектов в макете
#ifdef APSTUDIO_INVOKED
terror this file is not editable by Microsoft Visual C++
#endif //APSTUDIO_INVOKED
/////////'11/1111/111/1111111111/1111111/1' I Ullll/lt'I'III'I•II/
I I / I I / / / / / I II t / / / I
II Add manually edited resources here...
^include "3dPlus.rc"
// Tank parts
I DX_HULL XO F re S \ T_hul 1. X
IDX_TURRET XOF res\turret.x
IDX_GON XOF res\gun.x
IDX_RADAR XOF res\radar.x
camo.bmp BITMAP res\camo.bmp
camousa.bmp BITMAP res\camousa.bmp // Звуковые эффекты
IDS_BANG WAVE res\bang.wav
/////////////////////////////////////////////////////////// //////////////////
Рисунок. 6-13. Размещение радара внутри фрейма

Башня
Тэг XOF, встречающийся в файле ресурсов, на самом деле можно заменить любой другой строкой. Я выбрал XOF лишь потому, что такое расширение используется в файлах описания фигур. Единственное место программы, где встречается строка XOF — функция C3dShape::Load, где эта строка используется для того, чтобы отличать XOF-файлы от других типов ресурсов.
Создание собственного контроллера движения
/b>
В класс танка вошли три функции, находящиеся в файле 3dTank.cpp и предназначенные для регулирования углов башни и пушки, а также для стрельбы:
#define D2R 0.01745329251994
void C3dTank::SetTurret(double angle)
{
if ((angle « 0) II (angle »= 360)) { angle = 0;
} double x = sin(angle * D2R);
double z = cos(angle * D2R);
m_turret.SetDirection(x, 0, z, &m_hull);
void C3dTank::SetGun(double angle) {
if (angle « 0) ( angle = 0;
} else if (angle »= 60) ( angle = 60;
> double у = -sin(angle * D2R);
double z = cos(angle * D2R);
m gun.SetDirection(0, у, z, &m turret);
}
void C3dTank::FireGun() {
PlaySound(MAKEINTRESOURCE(IDS_BANG), AfxGetResourceHandie(), SND_RESOURCE) ;
}
Как видите, чтобы определить положение башни и пушки, мы вычисляем вектор направления. Затем мы задаем направление объекта по отношению к его родителю', кстати говоря, именно так функция SetDirection действует по умолчанию. Но я хотел сделать свой код максимально простым и очевидным, поэтому при каждом вызове передаю дополнительный аргумент — эталонный фрейм.
Танк готов. Осталось научиться управлять им.
Контроллер танка
Большая часть кода контроллера находится в классах C3dWnd и C3dController. Чтобы создать собственный контроллер, необходимо лишь ввести новый класс, производный от CSdController, переопределить в нем функцию OnUpdate и установить новый контроллер в своем приложении. Однако перед тем, как писать функцию OnUpdate, следует распределить параметры джойстика
/b> Д1' Глава 6. Перемещение объектов в макете
по выполняемым функциям. Конфигурация, на которой я остановился, приведена в табл. 6-3.
Таблица 6-3. Управление танком
Входной параметр Параметр танка
у Скорость
х Поворот
r Поворот POV (кнопка выбора вида) Направление башни
Кнопки 3 и 4 Подъем и опускание пушки
Кнопка 1 Выстрел из пушки
Я решил использовать параметры х и г для поворотов, чтобы даже при наличии самого простого джойстика с двумя осями можно было управлять танком. Я выбрал для этого приложения джойстик SideWinder Pro — он дает более реалистичные ощущения, чем SpaceBall. К тому же кнопка выбора вида, находящаяся на рукояти джойстика, замечательно подходит для поворотов башни.
Определившись с управлением, можно писать программу. Весь код контроллера состоит из двух функций:
CTankCtrl::CTankCtrl () (
m_dGunAngle = 25;
m_bWasFire = FALSE;
}
void CTankCtrl::OnUpdate(_3DIMPUTSTATE& st, C3dFrame* pFrame) {
// Задать скорость (руководствуясь значением у)
double v = st.dY / 2;
// Определить текущее положение C3dVector pos;
pFrame-»GetPosition (pos) ;
// Получить текущий вектор направления C3dVector dir, up;
pFrairie-»GetDirection(dir, up) ;
// Определить новое направление (с учетом
// параметров х и г)
double dr = -st.dX + -st.dR;
C3dMatrix r;
r.Rotate(0, dr * 3, 0) ;
dir = r * dir;
Создание собственного контроллера движения 'т^ 159
// Умножить вектор направления на скорость, // чтобы определить смещение танка C3dVector ds = dir * v;
// Задать новое положение и направление pos += ds;
pFrame-»SetPosition (pos) ;
pFrame-»SetDirection (dir) ;
// Воспользоваться информацией POV для задания
// ориентации башни.
// Для этого необходимо работать с объектом C3dTank,
// а не CSdFrame.
C3dTank* pTank = (C3dTank*) pFrame;
ASSERT (pTank-»IsKindOf (RUNTIME_CLASS (C3dTank) ) ) ;
if (st.dPov »= 0) { pTank-»SetTurret (st.dPov) ;
}
// Кнопки З и 4 поднимают и опускают пушку if (st.dwButtons & 0х04) {
m_dGunAngle += 0.1;
» if (st.dwButtons & 0х08) (
m dGunAngle -= 0.1;
} if (m_dGunAngle « 0) {
m dGunAngle =0;
} else if (m_dGunAngle » 45) {
m dGunAngle = 45;
} pTank-»SetGun (m dGunAngle);
// Проверить, не пора ли стрелять if (st.dwButtons & 0х01) { if (!m_bWasFire) 1 pTank-»FireGun () ;
m_bWasFire = TRUE;
} } else (
m_bWasFire = FALSE;
} }
Конструктор лишь инициализирует некоторые локальные данные; вся настоящая работа выполняется в функции Onllpdate. Параметр у задает текущую скорость. Текущая позиция и направление танка хранятся в объектах C3dVector. Параметры х и г определяют матрицу поворота, которая задает новую ориента-
/b> '^р? Глава 6. Перемещение объектов в макете
цию вектора направления. Вектор направления умножается на скорость — полученный вектор смещения складывается с вектором прежнего положения танка. Затем мы перемещаем танк в новое положение и задаем для танка новое направление.
Кнопка выбора вида определяет направление башни. Мы проверяем состояние кнопок 3 и 4, и если они нажаты, то угол подъема пушки изменяется на небольшую величину. Если держать одну из этих кнопок нажатой, башня будет медленно подниматься или опускаться.
Остается лишь учесть кнопку стрельбы. Проверка локальной переменной m_bWasFire предотвращает повторные выстрелы при нажатой кнопке — автоматическое оружие в США запрещено.
Окончательная сборка приложения
За основу приложения Tank был взят код приложения Moving. Я удалил ненужные команды меню и заменил текущую фигуру объектом CSdTank. Кроме того, я включил в макет фоновое изображение. Ниже приведен фрагмент кода, в котором происходит настройка главного окна приложения:
int CMainFrame::OnCreate(LPCREATESTRUCT IpCreateStruct) {
// Загрузить фоновое изображение m_imgBkgnd.Load(IDB BKGND) ;
NewScene() ;
ASSERT(m_pScene) ;
// Создать объект-контроллер m_pController = new CTankCtrl;
m_pController-»Create (&m wnd3d,
OnGetCtrlFrame,
this) ;
// Восстановить конфигурацию контроллера m_pController-»SelectDevice (m_iObjCtrlDev) ;
return 0;
}
Функция NewScene создает макет и задает начальные условия
BOOL CMainFrame::NewScene() (
// Удалить макет, если он уже существует if (m_p3cene) {
m_wnd3d.SetScene(NULL) ;
delete m_pScene;
m_pScene = NULL;
?
Создание собственного контооллеоа движения
/b>
// Создать исходный макет m_pScene = new CSdScene;
if ( !m_pScene-»Create() ) return FALSE;
// Задать источники света C3dDirLight dl;
dl.Create (0.8, 0.8, 0.8);
m pScene-»AddChild(&dl) ;
dl.SetPosition(-2, 2, -5);
dl.SetDirection(l, -1, 1);
m_pScene-»SetAmbientLight(0.4, 0.4, 0.4);
// Установить положение и направление камеры // в исходное состояние m_pScene-»SetCameraPosition (C3dVector (0, 5, -25));
m_pScene-»SetCameraDirection (C3dVector (О, О, 1));
m_wnd3d.SetScene(m_pScene) ;
// Задать фоновое изображение m pScene-»SetBackground(&m_imgBkgnd) ;
// Разместить танк в макете if (!m_pTank) m_pTank = new C3dTank;
m_pScene-»AddChild(m_pTank) ;
m_pTank-»SetPosition(0, 0, 0) ;
m_pTank-»SetDirection(0, 0, 1) ;
return TRUE;
}
Если танк уедет за край окна и потеряется, можно выполнить команду Fite ¦New, чтобы вызвать функцию NewScene и начать все заново. Осталось сказать о последнем изменении, внесенном мной, — когда контроллер запрашивает указатель на фрейм, с которым он должен работать, функция OnGetCtrlFrame возвращает ему указатель на танк:
C3dFrame* CMainFrame::OnGetCtrlFrame(void* pArg) (
CMainFrame* pThis = (CMainFrame*) pArg;
ASSERT(pThis) ;
ASSERT <pThis-»IsKindOf(RUNTIME_CLASS (CMainFrame) ) ) ;
return pThis-»m_pTank;
}
Обратите внимание — хотя функция должна возвращать указатель на C3dFrame, на самом деле она передает указатель на объект C3dTank. Мы пользуемся этим обстоятельством в функции Onllpdate, приведенной на стр. 144. Если раньше вам могло показаться, что преобразование указателя на C3dFrame в указатель на
/b> Ш^ Глава 6. Перемещение объектов в макете
CSdTank выглядит сомнительно, то теперь нетрудно убедиться, что мы имели полное право поступать таким образом.
Пора в дорогу
Хватит возиться с самолетами, часами и танками. Пойдем дальше и посмотрим, как выбираются объекты в макете.
Кто бы мог подумать: трехмерный
Предисловие
Кто бы мог подумать: трехмерный синтез с наложением текстур в реальном времени на компьютере PC стоимостью в $1000! Такое стало возможным благодаря сочетанию невероятного роста вычислительной мощности процессоров с изощрениями разработчиков пакетов трехмерного синтеза, и, вероятно, отчасти благодаря появлению дешевых акселераторов трехмерной графики (хотя и без них, на «чистом» процессоре можно добиться превосходных результатов). Остается сущий пустяк — реализовать этот потенциал. Помимо самых разнообразных программных библиотек для работы с трехмерной графикой, рынок PC прямо-таки завален аппаратными ЗО-акселераторами. Несчастные разработчики игр, у которых и так хватало головной боли с совместимостью для всех обычных видеокарт, заведомо не смогут угнаться за дьявольской фантазией производителей ЗО-акселераторов.
Однако на сцене появляется Direct3D. Пакет выполняет функции посредника:
он объединяет схожие возможности различных аппаратных средств в едином API. Кроме того, Direct3D содержит собственный, вполне достойный механизм трехмерной визуализации (rendering). Отныне вам, разработчику игр (а может быть, дизайнеру САПР или «воскресному» программисту), остается лишь вызвать несколько простых функций, чтобы на экране, как по волшебству, заплясали трехмерные фигуры.
И все же без ложки дегтя дело не обходится — исходный вариант Direct3D проектировался в расчете на старый добрый язык С, а правоверные программисты нашего времени предпочитают объектно-ориентированный стиль популярного C++. В сущности, первое, что пытается сделать любой квалифицированный программист на C++, когда он сталкивается с новым API на языке С, — это создать классы-оболочки на C++.
Итак, мы сталкиваемся с двумя серьезными проблемами. В наши дни программисту приходится не столько писать свой собственный код, сколько думать о том, какую системную функцию следует вызвать. Кроме того, программисты желают «завернуть» API на языке С в «покрывало» C++. Познакомьтесь с Найджелом Томпсоном. Он решил за вас обе проблемы. С использованием его библиотеки, написанной на C++, вы сможете легко создавать изображения, для которых бы иначе потребовался убийственный объем кода на С с «сырыми» вызовами Direct3D.
Вы, читатель этой книги, выигрываете во многих отношениях. Вы знакомитесь с трехмерной графикой и можете работать с ней из C++. Direct3D позволяет создавать картинки независимо от того, какую комбинацию программных/аппаратных средств для трехмерной графики вы установили у себя на этой неделе. Отныне следует сосредоточить свое внимание на том, что рисовать, а не на том, как это делать. Найджел, впрочем, тоже выигрывает, поскольку вы купили его книгу. И я выигрываю тоже — я люблю игры, а теперь можно надеяться на появление новых хороших игрушек. Так что принимайтесь за дело!
Джим Блинн, специалист по компьютерной графике, Microsoft
Преобразования
Глава 5 Преобразования
Матрицы и преобразования

Большая часть преобразований, которыми мы будем пользоваться, может быть описана в виде вещественной матрицы 3х3. Однако работа с матрицами 3х3 несколько усложняет вычисления, поскольку некоторые преобразования выполняются не так, как другие. Например, перенос реализуется сложением элементов матрицы, а поворот — умножением. Тем не менее, если вставить элементы матрицы 3х3 в матрицу 4х4 и должным образом заполнить свободные места, все преобразования можно будет выполнять посредством операции матричного умножения, поэтому для описания преобразований мы будем пользоваться матрицами 4х4. Если вы незнакомы с однородной системой координат, которая применяется при описании преобразований в трехмерном пространстве (а кто с ней знаком, кроме математиков?), вы наверняка чувствуете себя сбитым с толку. Давайте немедленно решим эту проблему и начнем с небольшого примера того, как пользоваться матрицами для преобразования координат точки в пространстве. Поскольку формулы для трехмерного случая оказываются довольно длинными, мы вместо этого рассмотрим упрощенный пример на плоскости — уверяю вас, в трехмерном пространстве он работает точно так же.
Двумерные координаты точки х, у в однородной системе координат представляются вектором следующего вида:
х
У 1
Матрица для переноса точки на плоскости выглядит следующим образом:
WlaTDHLlbl и поеобпазпняния "it!!® 121
1 0 dx О 1 dy 00 1
где dx — смещение точки по оси х, а dy — смещение по оси у. Теперь давайте умножим исходный вектор на эту матрицу и посмотрим, что у нас получится. При умножении матрицы на вектор-столбец каждый элемент вектора-результата представляет собой сумму элементов соответствующей строки матрицы, умноженных на элементы исходного вектора:
"1 0 dx] Гх] Г1 * х + 0 - у + 1 * dx] Гх + dx" 01dyxy=0*x+l*y+l*dy=y+dy 001 1 0 * х + 0 * у + 1 • 1 1
Как видит! при умножении вектора на матрицу переноса получается вектор, смещение которого в точности соответствует желаемому. Гениально! Когда я впервые научился пользоваться однородными координатами для сведения всех преобразований к умножению матриц, на меня это произвело глубочайшее впечатление. Впрочем, даже если вы не особенно потрясены, по крайней мере матричные преобразования становятся несколько более понятными.
Теперь давайте попробуем применить полученные знания на практике и воспользуемся объектом C3dMatrix, содержащим массив вещественных величин 4х4, для переноса вектора. Чтобы вы получше представляли себе класс C3dMatrix, привожу исходный текст его конструктора:
C3dMatrix::C3dMatrix()
{
т_00=1.0; т_01°0.0; т_02=0.0; т_03=0.0;
т_10=0.0; т_11=1.0; т_12=0.0; т_13=0.0;
т_20=0.0; т_21=0.0; т_22=1.0; т_23=0.0;
т_30=0.0; т_31=0.0; т_32=0.0; т_33=1.0;
}
В исходном состоянии, задаваемом в конструкторе, эта матрица является матрицей идентичного преобразования, или единичной матрицей. Если умножить вектор на такую матрицу, он не изменится. Приведенный ниже фрагмент, использующий объект C3dMatrix, осуществляет перенос вектора х, у, z со смещениями координат dx, dy, dz:
C3dVector v (х, у, z) ;
C3dMatrix т;
т.Translate(dx, dy, dz);
v = т * v;
Объект C3dVector инициализируется элементами исходного вектора. Затем, после конструирования объекта C3dMatrix (который в первоначальном состоянии совпадает с матрицей идентичного преобразования), вызывается его функция
/b>
Глава 5. Поеобоазования
Translate для занесения в матрицу преобразования переноса. Наконец, вектор умножается на матрицу, и результат присваивается исходному вектору.
Не следует полагать, будто функция C3dMatrix: translate просто инициализирует матрицу; как нетрудно убедиться по приведенному ниже фрагменту, на самом деле она комбинирует преобразование переноса с любыми преобразованиями, уже занесенными в матрицу:
void C3dMatrix::Translate(double dx, double dy, double dz)
{
C3dMatrix tx( 1, О, О, О,
О, 1, О, О, О, 0, 1, О, dx, dy, dz,l);
*this *= tx;
Временная матрица инициализируется элементами для преобразования переноса. Затем текущая матрица умножается на временную матрицу переноса, а результат снова присваивается текущей матрице.
Пользуясь различными функциями класса C3dMatrix, можно комбинировать в одной матрице сразу несколько преобразований и затем применять их к нужному количеству векторов. Удобно также создать отдельные объекты C3dMatrix, каждый из которых соответствует отдельному преобразованию, и просто перемножить их для получения итогового преобразования:
mFinal = ml * m2 * m3;
Преобразования трехмерных объектов
Теперь давайте посмотрим, как матричные преобразования используются на практике, при работе с трехмерными объектами. Чтобы применить матрицу преобразования к объекту C3dShape, вовсе не нужно заниматься умножением. Вместо этого следует скомбинировать новое преобразование с текущим, хранящимся во фрейме объекта. Вспомните — фрейм, определяющий положение и ориентацию объекта в макете, на самом деле представляет собой преобразование, применяемое ко всем точкам фигуры. Кроме того, фрейм объекта является потомком другого фрейма, расположенного выше в иерархии, и для определения окончательного положения объекта необходимо скомбинировать результаты всех преобразований в иерархии фреймов. Мы собираемся изменить преобразование, хранящееся во фрейме объекта, расположенном где-то внизу иерархии фреймов, пример которой изображен на Рисунок 5-1.
Изображенный на Рисунок 5-1 сложный объект состоит из двух фигур, каждая из которых обладает собственным фреймом и визуальным элементом. Для преобразования всего объекта следует модифицировать объединяющий фрейм, который является общим родителем для фреймов обоих компонентов.
Преобразование фрейма можно изменить тремя способами, а именно включив новое преобразование перед текущим, после него или же заменить им текущее преобразование. Как определить, какой из способов следует использовать в
Поеобоазования тоехмеоных объектов vis' 123
Рисунок. 5-1. Иерархия фреймов

каждом конкретном случае? Я надеюсь, что после знакомства с примерами вы и сами найдете ответ на этот вопрос.
Все преобразования, которые мы будем рассматривать, содержатся в приложении TransFrm. Для демонстрации я выбрал самолет, поскольку его положение в макете и ориентация определяются с первого взгляда. На Рисунок 5-2 изображено начальное состояние самолета, находящегося в начале координат.
Окно приложения до применения преобразований

/h2>
Глава 5. Преобразования
Перенос
Первый тип рассматриваемых нами преобразований — перенос. Переносом называется простое прямолинейное перемещение объекта в одном направлении. Для переноса объекта следует прибавить к его координатам х, у и z величины смещений. На Рисунок 5-3 изображен результат переноса по оси х.
Рисунок. 5-3. Перенос по оси х

Фрагмент программы, в котором был осуществлен этот перенос, выглядит следующим образом:
void CMainFrame::OnEditTranslatex() (
if (!m_pCurShape) return;
C3dMatrix m;
m.Translate (2, О, О);
m_pCurShape-»AddTransform(m, D3DRMCOMBINE_AFTER) ;
}
Сначала мы создаем объект C3dMatrix для хранения матрицы переноса (в данном случае, для смещения на 2 единицы вдоль оси х). Затем преобразование применяется к текущей фигуре. Обратите внимание на аргумент D3DRMCOMBINE_AFTER, который указывает на необходимость применения преобразования после любых существующих преобразований. Другими словами, после завершения всех преобразований появляется дополнительный перенос объекта вдоль оси х.
Поворот
Теперь давайте развернем наш самолет, расположенный в начале координат, на 45 градусов вокруг оси у. Результат изображен на Рисунок 5-4.
Преобразования трехмерных объектов
/b>
Рисунок. 5-4, Поворот вокруг оси у

Ниже приведен текст функции, в которой выполняется поворот:
void CMainFrame::OnEditRotatey() {
if (!m_pCurShape) return;
C3dMatrix m;
m.RotatefO, 45, 0);
m_pCurShape-»AddTransform(m, D3DRMCOMBINE AFTER);
Масштабирование
Еще один тип преобразований объекта — масштабирование, увеличивающее или уменьшающее его размеры. Самое интересное заключается в том, что для каждой оси можно выбрать свой коэффициент масштабирования. На Рисунок 5-5 показано, как будет выглядеть самолет после растяжения только по осям х и у.
Наш самолет выглядит по меньшей мере странно! Результат последующего применения аналогичного масштабирования по оси z изображен на Рисунок 5-6.
Масштабирование в программе мало чем отличается от других, рассмотренных выше преобразований. Ниже приведен пример того, как выполняется масштабирование только по оси х:
void CMainFrame::OnEditscalex() {
if (!m_pCurShape) return;
C3dMatrix m;
m.Scale(2.0, 1.0, 1.0);
m_pCurShape-»AddTransform(m, D3DRMCOMBINE AFTER);
}
/b>
Глава 5. Преобразования
Рисунок. 5-5. Масштабирование объекта по осям х и у

Объект после равномерного масштабирования по осям х, у и z

Обратите внимание на то, что коэффициенты масштабирования по осям у и z равны 1, а не 0. Если присвоить им нулевые значения, вам будет нелегко рассмотреть свои объект!
/h2>
Порядок преобразований
Мы рассмотрели отдельные преобразования переноса, поворота и масштабирования. Теперь давайте посмотрим, что происходит при выполнении серии последовательных преобразований. Начнем с переноса вдоль оси х, за которым следует поворот вокруг оси у. Результат изображен на Рисунок 5-7.
Рисунок. 5-7. Перенос вдоль оси х, за которым следует поворот вокруг оси у

Совпадает ли такой результат с тем, что вы ожидали увидеть? Текст функции приведен ниже:
void CMainFrame::OnEditTranrot() {
if (!m_pCurShape) return;
C3dMatrix m;
m.Translate(3, 0, 0) ;
m.Rotate(0, 45, 0) ;
m_pCurShape-»AddTransform(m, D3DRMCOMBINE_AFTER) ;
Как видите, мы осуществили перенос на 3 единицы вдоль оси х, после чего развернули объект на 45 градусов вокруг оси у. Во время поворота самолет находился на расстоянии в 3 единицы от начала координат. Следовательно, самолет описал дугу в 45 градусов по окружности радиусом в 3 единицы.
Давайте повторим те же самые преобразования, но на этот раз изменим их порядок. Результат изображен на Рисунок 5-8.
Как видите, результат значительно отличается от предыдущего. На этот раз все выглядит так, словно после переноса самолет развернулся вокруг собственной оси, а не вокруг оси у макета.
/h2>
Глава 5. Поеобоазования
Рисунок. 5-8. Поворот вокруг оси у, за которым следует перенос вдоль оси х

Только что мы сделали важное открытие: порядок применения преобразований чрезвычайно важен. Кроме того, мы выяснили, что для того, чтобы повернуть объект вокруг оси макета, следует применять поворот после всех переносов;
для того, чтобы объект вращался вокруг его собственной оси, поворот следует применить до переносов. Это необходимо знать, если вы хотите в полной мере контролировать положение всех объектов. В главе 6 мы воспользуемся этой методикой для имитации полета.
В нашем приложении имеются команды меню, поворачивающие объект вокруг осей макета, по аналогии с фрагментом на стр. 128. Сюда также включены команды для выполнения поворотов вокруг собственной оси объекта. Ниже приводится пример поворота вокруг оси у объекта:
void CMainFrame::OnEditRobjy() {
if (!m_pCurShape) return;
C3dMatrix m;
m.Rotate(0, 45, 0) ;
m_pCurShape-»AddTransform(m, D3DRMCOMBINE_BEFORE) ;
С первого взгляда кажется, что данный фрагмент полностью совпадает с приведенным на стр. 126, поболее внимательное рассмотрение показывает, что поворот на этот раз выполняется до текущего преобразования (D3DRMCOMBINEJ3EFORE), а не после него.
Возвращение на базу
Полет подходит к концу, и настало время возвращаться обратно. Наше приложение содержит команду Edit ¦ Reset, которая возвращает объект в начало координат
Преобразования трехмерных объектов
/b>
и возвращает ему исходное положение и ориентацию. Ниже приведена соответствующая функция:
void CMainFrame::OnEditReset()
{
if (!m_pCurShape) return;
C3dMatrix m;
m_pCurShape-»AddTransform(m, D3DRMCOMBINE_REPLACE) ;
}
Вам может показаться, что здесь допущена какая-то ошибка — ведь для матрицы вообще не задано никакого преобразования. Однако на самом деле именно это нам и нужно! Обратите внимание на использование аргумента D3DRMCOMBINE_REPLACE, заменяющего любое текущее преобразование новой матрицей. Конструктор матрицы инициализирует ее элементами единичной матрицы; заменяя текущую матрицу фрейма на матрицу идентичного преобразования, мы возвращаем объект в исходное состояние.
Экспериментируйте!
В приложении имеется окно диалога, открываемое командой Edit ¦ Transform Shape. Оно используется для задания произвольных преобразований переноса, поворота и масштабирования. В любом случае можно указать, следует ли применять новое преобразование до текущего, после него или же заменить текущее преобразование новым. Несколько опытов с окном диалога Transforms, изображенным на Рисунок 5-9, заполнят все возможные пробелы в вашем понимании того, как же комбинируются преобразования.
Рисунок. 5-9. Окно диалога Transforms

Житейские мелочи
На самом деле мы рассмотрели не все преобразования, которые могут быть применены к фигуре, а ограничились лишь самыми полезными из них. Я хотел бы закончить эту главу небольшим лирическим отступлением и продемонстрировать вам еще одно, последнее преобразование. Сдвигом называется преобразование, которое перекашивает объект в боковом направлении. Например, положите на стол колоду аккуратно сложенных карт и толкните ее верх в сторону, чтобы края
/b>
Глава 5. Преобразования
колоды по-прежнему оставались прямыми, но не были перпендикулярны столу, как показано на Рисунок 5-10.
Рисунок. 5-10. «Сдвинутая» колода карт

Итак, мы применили к колоде преобразование сдвига. На Рисунок 5-11 показано, что получится в результате применения сдвига к нашему самолету.
Рисунок 5-П. Результат применения сдвига
Чтобы вам было легче разглядеть самолет после сдвига, я немного увеличил его, применив перед сдвигом масштабирование с одинаковыми коэффициентами по всем трем осям. Я не смог придумать для сдвига достойного применения в трехмерном приложении, но наверняка вы сможете это сделать, поэтому я привожу текст функции, выполнившей преобразование сдвига на Рисунок 5-11:
void CMainFrame::OnEditShear() (
if (!m_pCurShape) return;
Til
Проверка попадания
Глава 7 Проверка попадания
Процесс выделения

Выделение объектов мышью выглядит очень естественно — пользователь наводит указатель мыши на объект и нажимает кнопку. Тем не менее приложению не так просто определить, какой же объект был выделен. Прежде всего, пользователь может применять мышь для манипуляций с объектами, поэтому сообщения, посылаемые Windows главному окну (о том, где находится указатель мыши и какая кнопка была нажата), должны попадать сразу в несколько мест. Обычно это делается следующим образом: некий центральный фрагмент программы перехватывает сообщения мыши и направляет их всем другим фрагментам, которым они могут понадобиться. Вы сохраняете текущее состояние мыши в глобальной переменной и позволяете всему коду непосредственно обращаться к ней. Альтернативный вариант — реализовать предложенную мной схему, то есть написать простую функцию, которая обрабатывает сообщения мыши и обращается к другим фрагментам приложения, уведомляя их о наступлении того или иного события.
Предположим, вы знаете, в какой точке экрана находится указатель мыши и что пользователь нажал кнопку, желая выделить объект в макете. Но как же определить, в каком объекте пользователь произвел щелчок мышью? Первым делом необходимо привести экранные координаты мыши к координатам клиент-ной области вашего окна. Затем вам фактически понадобится обратить проекционное преобразование, которым пользуется механизм визуализации, и перевести двумерные координаты на вашем экране в пространственные. Сделать это не так просто, как может показаться с первого взгляда. Как мы вскоре увидим, меха-
Процесс выделения 'тЦЦ 165
низм DirectSD способен выполнить подобную процедуру за нас — в определенной степени. Вместо того чтобы преобразовать экранные координаты мыши в трехмерные, он выдает список всех объектов, которые находятся ниже выбранной точки. Кроме того, список сортируется по глубине, чтобы вы могли определить, какой объект находится перед остальными — именно его (будем надеяться!) и пытается выделить пользователь. Все эти операции требуют довольно сложного жонглирования матрицами преобразований.
В наших приложениях-примерах в любой момент времени разрешается выделить только один объект. Подобное ограничение упрощает код, поскольку можно завести переменную-указатель (m_pCurShape), которая ссылается на текущий выделенный объект или равна NULL, если выделенных объектов нет. Позднее мы увидим, что в наших приложениях также поддерживается концепция текущей выделенной грани объекта — грани текущего выделенного объекта, над которой находился указатель мыши в момент выделения.
Для того чтобы реализовать проверку попаданий в приложениях-примерах, мне пришлось включить в них немало фрагментов, рассредоточенных по разным местам. В последующих разделах я постараюсь объяснить, где должен находиться тот или иной фрагмент и как он работает. Если вы не следите за моими объяснениями и хотите самостоятельно разобраться, как работает программа, советую запустить приложение под отладчиком, установить точку прерывания в функции C3dWnd::OnWndMsg (файл 3dWnd.cpp в библиотеке 3dPlus) и следить за выполнением программы. Еще раз хочу подчеркнуть, что эту задачу можно было решить множеством способов, причем выбранное мною решение, вероятно, ничуть не лучше любого другого. Если вам кажется, что ваша собственная идея даст сто очков вперед предложенной мною, — наверное, вы правы и именно ей вам следует пользоваться в ваших программах.
Выделение всего объекта
Основная часть задачи выделения объектов выполняется механизмом визуализации в рамках интерфейса ракурса. Тем не менее перед тем, как приступать к изучению его работы, я бы хотел кратко описать последовательность событий, происходящих с момента щелчка мышью на объекте макета. Мы пройдемся по различным фрагментам программы, начиная с трехмерного окна, в котором отображается макет.
Перед тем как ваше приложение сможет воспользоваться средствами проверки попадания, заложенными в классе C3dWnd, оно должно вызвать функцию, назначение которой — установка уведомляющей функции, вызываемой при каждом попадании в объект. Наверное, нет особого смысла возиться с проверкой попаданий, если потом ничего не делать с ее результатами. Начнем с создания главного обрамленного окна программы:
int CMainFrame::OnCreate(LPCREATESTRUCT IpCreateStruct) {
// Разрешить выделение объектов мышью m_wnd3d.EnableMouseSelection(OnSelChange, this);
}
/b> lly Глава 7. Проверка попадания
В приведенной выше строке программы устанавливается уведомляющая функция OnSelChange. Функция OnSelChange является статической функцией класса CMainFrame, и потому значение указателя this для нее не определено. Как мы вскоре увидим, второй аргумент функции EnableMouseSetection передается в виде аргумента рАгд при вызове уведомляющей функции — в данном случае мы передаем указатель на объект C++ (если этот момент покажется вам непонятным, просмотрите код функции EnableMouseSelection в файле C3dWnd.cpp). Давайте посмотрим, как щелчок мышью обрабатывается в классе C3dWnd — это снова приведет нас к обсуждению уведомляющей функции. Ниже приведен фрагмент обработчика сообщений окна, связанный с проверкой попадания:
BOOL C3dWnd::OnWndMsg(UINT message, WPARAM wParam,
LPARAM IParam, LRESULT* pResult ) {
// Разрешено ли выделение объектов мышью?
if (m_bEnableMouseSelection
&& (message == WM_LBUTTONDOWN)) (
CPoint pt(LOWORDfIParam), HIWORD(IParam));
C3dShape* pShape = HitTest(pt);
if (m_p3elChangeFn) {
// Вызвать уведомляющую функцию m_pSelChangeFn(pShape, pt, m pSelChangeArg);
} }
return CWnd::OnWndMsg(message, wParam, IParam, pResult);
}
Если выделение мышью было разрешено (рассматривается именно этот случай), мы создаем объект CPoint по координатам мыши, содержащимся в сообщении WM_LBUTTONDOWN, а затем вызываем функцию HitTest, чтобы определить, произошло ли попадание в фигуру. Результат проверки (который равен NULL, если под мышью не оказалось ни одного объекта) возвращается приложению через уведомляющую функцию (которая была указана при разрешении выделения мышью). Давайте посмотрим, как уведомляющая функция используется в приложении:
void CMainFrame::OnSelChange(C3dShape* pShape, CPoint pt,
void* pArg) (
// Получить указатель на класс
CMainFrame* pThis = (CMainFrame*) pArg;
ASSERT(pThis) ;
ASSERT (pThis-»IsKindOf (RUNTIME_CLASS (CMainFrame) ) ) ;
if (pShape) {
// Убедиться, что попадание пришлось
Выделение всего пбъеш-а тТО 1&7
// не в рамку выделения и не в фигуру-указатель if ( !pShape-»IsPartOЈ (pThis-»m_pSelBox)
&& !pShape-»IsPartOf (pThis-»m_pHitPtr) ) {
// Определить грань, в которую мы попали
C3dViewport* pViewport =
pThis-»m_wnd3d.GetStage() -»GetViewport
p3hape-»HitTest (pt, pViewport,
&pThis-»m_iHitFace, &pThis-»m_vHitPoint) ;
1 .'. i ^ i * \
pShape = NULL;
}
i
I / Сделать выделенную фигуру текущей pThis-»MakeCurrent (pShape) ;
}
Выделенный объект передается функции MakeCurrent, которая рисует вокруг него рамку, чтобы отличить от других объектов (мы подробнее рассмотрим функцию MakeCurrent на стр. 177). Самая важная особенность этого фрагмента заключается в том, что 41ункция OnSelChange является статической, и потому, как было сказано выше, не имеет указателя this. Мы справились с данным затруднением, передавая адрес объекта C++ в качестве аргумента функции, разрешившей выделение объектов мышью (EnableMouseSelection). Значение, полученное уведомляющей функцией, преобразуется к типу указателя на наш класс. Хитро, не правда ли? Реализация косвенного вызова (callback) функции класса требует несколько больших усилий, поэтому уведомляющая функция была сделана статической для упрощения программы.
Теперь давайте более подробно рассмотрим, как же происходит проверка попадания. Функция C3dWnd::HitTest просто передает запрос ракурсу:
// Проверить на попадание в видимый объект C3dShape* C3dWnd::HitTest(CPoint pt) (
ASSERT(m_p3tage) ;
return m_pStage-»GetViewport ()-»HitTest (pt) ;
}
Фактическая проверка попадания производится в классе ракурса (код которого находится в файле 3dStage.cpp):
C3dShape* C3dViewport::HitTest(CPoint pt) {
IDirect3DRMPickedArray* pIPickArray = NULL;
/b> ЯНУ Глава 7. Поовеока попадания
ASSERT(m_pIViewport) ;
m_hr = m_pIViewport-»Pick(pt.x, pt.y, SpIPickArray);
if (FAILED(m_hr)) return NULL;
// Проверить, есть ли в массиве элементы if (pIPickArray-»GetSize () == 0) { pIPickArray-»Release () ;
return NULL;
)
// Получить первый (верхний) элемент IDirect3DRMVisual* pIVisual = NULL;
IDirect3DRMFrameArray* pIFrameList = NULL;
m hr = pIPickArray-»GetPick(0, SpIVisual, SpIFrameList, NULL) ;
ASSERT(SUCCEEDED(m_hr)) ;
ASSERT(pIVisual) ;
ASSERT(pIFrameList) ;
// Получить последний фрейм в списке IDirect3DRMFrame* pIFrame - NULL;
pIFrameList-»GetEiement (pIFrameList-»GetSize () - 1, &pI Frame);
ASSERT(pIFrame) ;
// Получить значение 'AppData' фрейма, // которое должно быть указателем на класс C++
C3ctShape* pShape = (C3dShape*) pIFrame-»GetAppData () ;
if (pShape) (
if(!pShape-»IsKindOf(RUNTIME_CLASS(C3dShape))) { pShape = NULL;
}
pIFrame-»Release () ;
pIFrameList-»Release () pIVisual-»Release () ;
pIPickArray-»Release ()
return pShape;
Первым делом мы требуем от интерфейса ракурса создать то, что в механизме визуализации называется списком выбора (pick list), то есть список всех визуальных элементов, находящихся под определенной точкой окна. Список визуальных элементов (pIPickArray) упорядочен так, чтобы верхний элемент находился в начале списка. Затем мы определяем значение указателя (pIVisual) на первый визуальный элемент и получаем по нему список фреймов (pIFrameList), к которым присо-
<::::й^
Выделение всего объекта т¦¦¦¦ 169
единен данный визуальный элемент. На Рисунок 7-1 показано, как связаны между собой объекты различных списков.
Список фреймов начинается с корневого фрейма (макета), за которым последовательно перечисляются все фреймы-потомки до самого последнего, содержащего отмеченный визуальный элемент.
Рисунок. 7-1. Структура списка выбора

Последнее, что нам осталось сделать, — извлечь значение переменной AppData из интерфейса фрейма. Объекты классов CSdFrame и C3dShape хранят в этой переменной значения своих указателей this. Мы преобразуем значение AppData к типу указателя на объект C3dShape и проверяем, не равен ли получившийся указатель NULL. Если не равен, то выполняется дополнительная проверка того, что данный указатель является указателем на объект C3dShape, с использованием функции MFC, возвращающей runtime-информацию о классе.
AppData может принимать значения трех типов: NULL, указатель на объект C3dFrame, указатель на объект C3dShape. Код проверки попадания работает лишь в том случае, если указатель ссылается на объект C3dShape и если объект класса C++, создавший визуальный элемент и фрейм, не был уничтожен. Деструктор класса C3dFrame (базового для C3dShape) присваивает AppData значение NULL, так что можно не опасаться случайного получения указателя на удаленный объект C++. Из всего сказанного следует, что функция HitTest полезна лишь при работе с теми трехмерными фигурами, с которыми связан текущий объект класса C3dShape.
Отображение выделения на экране
Если запустить приложение Select и щелкнуть на каком-нибудь объекте, вокруг последнего появляется рамка, похожая на изображенную на Рисунок 7-2.
Рамка расположена таким образом, чтобы показать граничную область объекта, то есть наименьшую кубическую область, содержащую все вершины объекта. Одна стрелка, состоящая из цилиндра и конуса, показывает вектор направления объекта, а другая стрелка (с конусом меньшей высоты) — его верхний вектор. Эти два вектора пересекаются в начале координат — точке объекта с координа-
/b>
Глава 7. Проверка попадания
тами О, О, О. В случае сферы на Рисунок 7-2, начало координат находится внутри объекта.
Рисунок. 7-2. Выделенный объект

Функция, рисующая рамку, несложна, хотя несколько длинна:
void CMainFrame::ShowSelection() {
// Определить граничную область объекта double xl, x2, yl, y2, zl, z2;
BOOL b = m_pCurShape-»GetBox (xl, yl, zl, x2, y2, z2);
ASSERT(b) ;
// Создать новую рамку вокруг фигуры m_pSelBox = new CSdShape;
double r = 0.03;
double re = r * 2;
C3dShape rl, r2, r3, r4, r5, r6, r7, r8, r9,
rIO, rll, rl2, rd, ru, cd, cu;
// Создать цилиндры, из которых состоит рамка
m_pSelBox-»AddChild(&r3) ;
r4.CreateRod(xl, y2, zl, x2, y2, zl, r) ;
m_pSelBox-»AddChild(&r4) ;
r5.CreateRod(x2, yl, zl, x2, y2, zl, r) ;
m_pSelBox-»AddChild(&r5) ;
r6.CreateRod(xl, y2, zl, xl, y2, z2, r) ;
^йй ВЫЛРПЙНИА япйгп nfi'^Rkra ''m^.
171
m_pSelBox-»AddChild(&r6) ;
r7.CreateRod(x2, y2, zl, x2, y2, z2, r) ;
m_pSelBox-»AddChild(&r7) ;
r8.CreateRod(x2, yl, zl, x2, yl, z2, r) ;
m_p3elBox-»AddChild(&r8) ;
r9.CreateRod(xl, yl, z2, xl, y2, z2, r) ;
m_pSelBox-»AddChild(&r9) ;
rIO.CreateRodfxl, yl, z2, x2, yl, z2, r) ;
m_pSelBox-»AddChild(&rlO) ; • rll.CreateRod(x2, yl, z2, x2, y2, z2, r) ;
m_pSelBox-»AddChild(&rll) ;
rl2.CreateRod(xl, y2, z2, x2, y2, z2, r) ;
m_pSelBox-»AddChild(&rl2) ;
//Создать цилиндры и конусы для отображения векторов rd.CreateRod(0, 0, 0, 0, 0, z2 * 1.2, r) ;
m pSelBox-»AddChild (&rd) ;
cd.CreateCone(0, 0, z2 * 1.2, re, TRUE, О, О, z2 * 1.4, 0, FALSE);
m_p3elBox-»AddChild(&cd) ;
ru.CreateRod(0, 0, 0, 0, y2 * 1.1, 0, r) ;
m_pSelBox-»AddChild(&ru) ;
cu.CreateCone(0, y2 • 1.1, 0, re, TRUE, 0, y2 * 1.2, О, О, FALSE) ;
m_pSelBox-»AddChild(&cu) ;
// Задать положение и ориентацию рамки
// в соответствии с положением и ориентацией фигуры
double х, у, z, xd, yd, zd, xu, yu, zu;
m pCurShape-»GetPosition (х, y, z) ;
m_pCurShape-»GetDirection (xd, yd, zd, xu, yu, zu) ;
m_pSelBox-»SetPosition (х, y, z) ;
m_pSelBox-»SetDirection (xd, yd, zd, xu, yu, zu) ;
// Присоединить рамку к текущей фигуре,
// чтобы обеспечить их совместное перемещение
m_pCurShape-»AddChild (m_pSelBox) ;
Граничная область фигуры используется для задания положения цилиндров, образующих рамку, и пар конус/цилиндр, которые изображают вектор направления и верхний вектор объекта. Все цилиндры и конусы присоединяются к одному объекту-рамке, имеющему то же положение и ориентацию, что и выделенный объект. Затем рамка присоединяется к выделенному объекту, чтобы она перемещалась вместе с ним.
Поскольку рамка также состоит из нескольких визуальных элементов, можно задать резонный вопрос — почему их нельзя выделить мышью? В уведомляющей функции на стр. 167 можно найти следующий оператор:
pShape-»IsPartOf (pThis-»m_pSelBox) 172 ад1'' Глава 7. Проверка попадания
Он является составной частью проверки, которая не позволяет выделять видимые элементы рамки. Функция IsPartOf проверяет, совпадает ли данный фрейм с фреймом-аргументом или с одним из его родителей. Другими словами, она проверяет, входит ли данный фрейм в иерархию другого фрейма.
Возможно, вы также вспомните мои слова о том, что видимые объекты, не имеющие присоединенных объектов C++, нельзя выделить. Если посмотреть на исходный текст функции, которая строит рамку, можно убедиться в том, что объекты C++, использованные при создании цилиндров и конусов, уничтожаются после создания рамки. Спрашивается, зачем же тогда нужна проверка IsPartOf? Дело в том, что один объект C++ все же остался — тот, на который ссылается переменная m_pSelBox. Чтобы заведомо устранить все возможные проблемы, мы идем на эту дополнительную проверку, хотя она и не является абсолютно необходимой. Кроме того, когда-нибудь в будущем функция, которая создает рамку, может измениться, и созданные объекты C++ не будут удаляться. Даже если это произойдет, выделение должно работать по-прежнему.
Мы научились выделять объекты. Запустите приложение Select, вставьте в текущий макет несколько объектов и пощелкайте на них мышью. При установке флажка Selection Box вы можете перемещать текущий выделенный объект и при этом видеть его рамку. Команда-флажок View ¦ Selection Box разрешает (и запрещает) отображение рамки в окне.
Выделение отдельной грани
Версия механизма визуализации, которой я пользовался для разработки программ к данной книге, не включала никакой поддержки для выделения отдельных граней, поэтому мне пришлось самостоятельно реализовать такую возможность. Я хочу показать вам, как я это сделал, чтобы продемонстрировать хороший пример работы с преобразованиями координат.
Задача состоит в следующем: зная координаты точки в трехмерном окне, необходимо определить грань объекта, находящуюся под данной точкой. Будем считать, что под точкой находится некоторый объект, который был найден с помощью методики, описанной в предыдущем разделе. На Рисунок 7-3 изображено графическое представление этой задачи.
Зная положение указателя мыши в окне, необходимо выяснить, какая грань объекта будет содержать проекцию точки. Более того, если под указателем мыши находится сразу несколько граней, необходимо выбрать ближнюю (с минимальным значением z).
Делается это следующим образом. Сначала мы получаем список всех граней объекта, а затем по очереди проектируем вершины каждой грани на плоскость вида и проверяем, лежит ли точка попадания внутри многоугольника, образованного проекциями вершин. Если будет найдена грань, содержащая точку попадания, необходимо выяснить, не находится ли она перед предыдущей найденной гранью. После проверки всех граней мы получим желаемый результат.
Единственное затруднение может возникнуть при проектировании вершин грани на плоскость вида; этот процесс состоит из трех шагов. Сначала необходимо преобразовать координаты каждой вершины из локальных координат фрейма в систему общих, «мировых» координат. Затем мировые координаты преобразуются в однородные координаты в плоскости вида. Наконец, вектор однородных координат преобразуется в точку окна.
Выделение отдельной грани 4¦^i 173
Рисунок. 7-3. Грань, спроектированная в трехмерное окно

Кроме того, необходимо как-то определить, находится ли точка внутри многоугольника вершин, спроектированных на плоскость вида. Вскоре мы увидим, как это делается, а пока давайте взглянем на функцию, в которой проверяются попадания в грань:
BOOL C3dShape::HitTest(CPoint pt,
C3dViewport* pViewport, int* piFace, D3DVECTOR* pvHit)
int iHitFace = -1;
double dHitZ = 0;
// Просмотреть список граней D3DVECTOR lv;
D3DVECTOR wv;
D3DRMVECTOR4D sv;
for (int i = 0; i « nFaces; i++) {
// Получить данные грани IDirect3DRMFace* piFace ° NULL;
m hr = pIFac@List-»GetElement (i, spIFace) ;
ASSERT;SUCCEEDED(m_hr)) ;
// Получить количество вершин и разместить массив // для хранения экранных координат int nVert = pIFace-»GetVertexCount () ;
ASSERT(nVert » 2) ;
/h2>
Глава 7. Проверка попадания
POINT* pScrnVert = new POINT [nVert];
// Преобразовать каждую вершину к экранным координатам double dZ = 0;
for (int v = 0; v « nVert; v++) {
// Получить вектор в локальных координатах
// (координатах фрейма)
m_hr = pIFace-»GetVertex(v, &lv, NULL) ;
ASSERT(SUCCEEDED(m_hr)) ;
// Преобразовать их в мировые координаты m_hr = m_pIFrame-»Transform(&wv, &lv) ;
ASSERT(SUCCEEDED(m_hr)) ;
// Преобразовать мировые координаты // в экранные
m_hr = pIViewport-»Transform(&sv, &wv) ;
ASSERT(SUCCEEDED(m_hr)) ;
// Преобразовать однородные координаты
// в абсолютные координаты пикселей
double w = sv.w;
if (w != 0) {
pScrnVert[v].x = (int) sv.x / w;
pScrnVert[v].у = (int) sv.y / w;
dZ += sv.z / w;
) else {
pScrnVert[v].x = 0;
pScrnVert[v].у = 0;
} } dZ /= nVert;
// Проверить, лежит ли точка попадания внутри // многоугольника на экране
if (::_3dPointInPolygon(pScrnVert, nVert, pt)) { if (iHitFace « 0) { iHitFace = i;
dHitZ = dZ;
} else (
if (dZ « dHitZ) {
iHitFace = i;
dHitZ •= dZ;
} } )
// Освободить грань после завершения delete [] pScrnVert;
Выделение отдельной грани 'тЩ 175
pIFace-»Release () ;
}
// Установить возвращаемое значение *piFace = iHitFace;
return TRUE;
}
Некоторые фрагменты кода опущены для экономии места, а также потому, что я хочу оставить их для дальнейшего обсуждения. Найдите то место, в котором координаты вершин преобразуются в однородный вектор. Давайте задержимся на нем.
Однородный вектор состоит из координат х, у, z и w. К чему так много координат, когда для представления точки в окне достаточно х и у? Причина заключается в том, что если вершина окажется очень близко к камере, то преобразование, отображающее координаты на плоскость вида, приведет к состоянию, близкому к делению на ноль, — разумеется, это нежелательно. Использование однородного вектора для представления результата позволяет избежать деления на ноль (поверьте мне на слово или покопайтесь в справочниках). При наличии однородного вектора мы вычисляем координаты точки в окне делением координат х, у и z на величину w. Если значение w равно нулю, мы считаем, что результат совпадает с точкой 0, 0. Но для чего нам нужно значение z? Разве точка на экране может обладать координатой z? Нет, не может, однако по координате z можно судить о положении на оси z той грани, которую мы проектируем на плоскость вида. С помощью этой информации мы выберем из множества возможных граней, содержащих точку попадания, ту, что находится ближе остальных.
Как видно из текста программы, далее мы проверяем, лежит ли точка попадания внутри многоугольника, образованного спроектированными вершинами, после чего смотрим, находится ли текущая грань впереди от уже найденных граней.
С проверкой принадлежности точки многоугольнику мне пришлось изрядно повозиться. Один из способов выяснить, лежит ли точка внутри многоугольника, — провести линию из данной точки в другую, находящуюся внутри многоугольника, и подсчитать, сколько раз эта линия будет пересекать его стороны. Нечетное количество пересечений означает, что точка находится за пределами многоугольника, как показано на Рисунок 7-4.
Рисунок, 7-4. Проверка принадлежности точки многоугольнику

/b> ily Глава 7. Проверка попадания
Сначала я поступил, немного глупо и решил написать код проверки самостоятельно. Я провел несколько часов, стараясь учесть все возможные случаи, и довольно близко подошел к ответу, когда здравый смысл все же взял верх. Я подумал, что на эту задача наверняка уже есть ответ и что найти его, вероятно, нетрудно. И оказался прав! Я отыскал нужный код в серии книг «Graphic Gems» (Academic Press) и приготовился вставить его в свою программу, когда меня посетила еще одна мысль. Вдруг такая функция уже имеется в Windows? После быстрого просмотра Microsoft Developer Library я нашел то, что искал, и окончательный вариант функции проверки (которая находится в файле SdMath.cpp) выглядит следующим образом:
BOOL _3dPointInPolygon(POINT* Points, int nPoints,
CPoint pt) {
HRGN hrgn = ::CreatePolygonRgn(Points, nPoints, WINDING);
ASSERT(hrgn) ;
BOOL b = ::PtInRegion(hrgn, pt.x, pt.y);
::DeleteObject(hrgn) ;
return b;
}
Я воспользовался интерфейсом GDI для создания многоугольной области, а затем завершил проверку функцией PtInRegion. Из всего этого я сделал один важный вывод: то, что я не пользуюсь функциями GDI в основной части своего проекта, еще не значит, что я вообще не должен пользоваться ими.
У меня получилось красивое, компактное решение. Я даже не стал возиться с измерением скорости работы, поскольку проверка происходит только в ответ на отдельное действие пользователя и даже низкая скорость проверки не приведет к заметной задержке. Если вам понадобится провести тысячу таких проверок, то, возможно, предложенный вариант решения уступит другим опубликованным алгоритмам.
Последнее замечание: реализованный мною код проверки попадания в грань не учитывает направления, в котором она обращена. Таким образом, теоретически можно попасть в грань, повернутую от пользователя и потому невидимую. Это может случиться тогда, когда за невидимой гранью имеется другая, видимая (если допустить, что до этого было обнаружено попадание в объект), поскольку код выбора, входящий в интерфейс, не возвращает объектов, у которых попадания произошли только в «теневые» грани.
В приложении Select грани, в которые происходит попадание, окрашиваются в красный цвет. Кроме того, в строке состояния выводится имя выделенного объекта, номер грани и координаты точки попадания в объекте (в следующем разделе мы узнаем, как определить координаты точки попадания). Все это происходит в приведенной ниже функции MakeCurrent:
void CMainFrame::MakeCurrent(C3dShape* pShape) f
HideSelection() ;
m pCurShape = pShape;
Выделение отдельной грани ''до 177
ShowSelectionf) ;
if (m_pCurShape != NULL) { if (m_iHitFace »= 0) {
Status("Selected: %s (%d @ %3.1f,%3.1f,%3 if)"
ni_pCurShape-»GetName () , m_iHitFace, ni_vHitPoint.x, m_vHitPoint.y, m_vHitPoint.z) ;
"PCurShape-»SetFaceColor(m_iHitFace, 1, О, О).
J Q -L SG { '
^ Status ("Selected: %s", m_pCurShape-»GetMame () ) ;
) else {
Status("No selection");
Определение точки попадания
Рисунок. 7-5. Проектирование точки попадания на объект

/h2>
Глава/. Проверка попадания
Для этого необходимо взять экранные координаты точки попадания и последовательно преобразовать их в однородный вектор, затем в мировые координаты и снова в локальные координаты объекта. Ниже приведен завершающий фрагмент функции C3dShape::HitTest:
// Вычислить положение точки попадания на грани // Подготовить вектор, описывающий точку экрана // В качестве z используется среднее значение. sv.x = pt.x;
sv.y = pt.y;
sv.z = dHitZ;
sv.w = 1.0;
// Привести к мировым координатам m hr = pIViewport-»InverseTransform ( &wv, &sv) ;
ASSERT(SUCCEEDED(m_hr)) ;
// Привести к локальным координатам фрейма m_hr = m_pIFrame-»InverseTransform(&lv, &wv);
ASSERT(SUCCEEDED(m_hr));
// Вернуть результат *pvHit == Iv;
Для упрощения кода я воспользовался грубой аппроксимацией значения z для точки на экране. В программе это значение определяется как среднее арифметическое координат z всех вершин, образующих грань проекции. На самом деле такой способ неверен, поскольку в нем никак не учитывается положение точки попадания в многоугольнике. Более корректный способ определения z изображен на Рисунок 7-6.
р
Рисунок. 7-6» Вычисление координаты z точки Р

Определение точки попадания ''"Щ 179
Точки А, В и С на Рисунок 7-6 — вершины грани. Соединим точку А с С, а В — с точкой попадания Р. Отношение длин отрезков АХ и ХС используется для вычисления координаты z точки Х по значениям координат z точек А и С. Отношение длин отрезков РВ и ХВ используется для вычисления координаты z точки Р по значениям координат z точек В и X. Оставляю вам завершить рассуждение в качестве домашнего задания.
В приложении Select имеется команда меню, которая показывает положение точки попадания на объекте (View ¦ Hit Point). Соответствующий фрагмент кода, расположенный в конце функции CMainFrame-:ShowSelection, создает конус и присоединяет его вершину к точке попадания, при этом ориентация конуса задается по нормали к выделенной грани:
// Получить точку попадания на фигуре
// и перейти от локальных координат к мировым
C3dVector vh = m pCurShape-»Transform(m vHitPoint);
// Определить направление нормали к грани ASSERT(m_pCurShape) ;
C3dVector vn = m_pCurShape-»GetFaceNormal (m iHitFace);
// Изменить длину нормали, прибавить нормаль к точке // попадания и преобразовать в мировые координаты C3dVector vx = vn * 0.5 + m vHitPoint;
vx = m pCurShape-»Transform (vx) ;
// Направить вершину конуса в точку попадания m_pHitPtr = new C3dShape;
m_pHitPtr-»CreateCone (vh.x, vh.y, vh.z, 0, FALSE, vx.x, vx.y, vx.z, 0.1, TRUE);
// Присоединить конус к фигуре m_pCurShape-»AddChild(m_pHitPtr) ;
}
}
Чтобы правильно определить положение конуса, необходимо привести локальные координаты объекта к системе мировых координат. На Рисунок 7-7 показано, как выглядит экран с конусом (кроме того, на цветной вкладке имеется изображение конуса, указывающего на выделенную сферу).
Вы можете легко убедиться в том, что усреднение координат z вершин неточно определяет положение точки попадания. Попробуйте выделить одну из боковых граней конуса. Вы увидите, что вершина конуса либо уходит внутрь грани, либо отходит на некоторое расстояние, вместо того, чтобы лежать точно на ней.
Проверка попадания на практике
Чтобы показать, как проверка попадания используется на практике, я создал приложение Blobs, в котором можно нарисовать на экране потрясающее космичес-
/b> ЦУ Глава 7. Проверка попадания
Рисунок. 7-7. Конус, показывающий положение точки попадания на объекте

кое существо, наподобие изображенного на Рисунок 7-8 (более качественная иллюстрация из приложения Blobs приведена на цветной вкладке).
Приложение Blobs

Приложение добавляет новое «пятно» к объекту, в точке где вы щелкаете мышью. Пятна на самом деле являются сферами, состоящими из четырех полос;
даже при небольшом количестве граней такая сфера выглядит неплохо. Чтобы создать это приложение, я взял пример Select, удалил все лишние команды меню
/h2>
Проверка попадания на практике
и изменил уведомляющую функцию, чтобы она добавляла к макету новые пятна. Новая функция выглядит следующим образом:
void CMainFrame::OnSelChange(C3dShape* pShape, CPoint pt,
void* pArg) {
// Получить указатель на объект класса
CMainFrame* pThis = (CMainFrame*) pArg;
ASSERT(pThis);
ASSERT(pThis-»IsKindOf (RUNTIME_CLASS(CMainFrame))) ;
if (pShape) {
// Определить, в какую грань пришлось попадание C3dViewport* pViewport =
pThis-»m_wnd3d.GetStage () -»GetViewport () ;
int iFace;
C3dVector vHit;
if (pShape-»HitTest (pt, pViewport, &iFace, &vHit) ) ( pThis-»AddBlob (pShape, vHit) ;
}
l
}
Как видно из листинга, после определения точки попадания вызывается функция AddBlob, которая присоединяет к фигуре новое пятно:
void CMainFrame::AddBlob(C3dShape* pShape, C3dVector& vHit) {
// Определить точку попадания
// и перейти от локальных координат к мировым
ASSERT(pShape) ;
C3dVector vh = pShape-»Transform (vHit) ;
// Создать новое пятно C3dShape* pBlob = new C3dShape;
pBlob-»CreateSphere (0.5, 4);
// Установить его центр в точке попадания pBlob-»SetPosition(vh) ;
// Присоединить пятно к фигуре pShape-»AddChild (pBlob) ;
// Включить новое пятно в список фигур,
// чтобы можно было проверять попадание в него
m_pScene-»m_ShapeList. Append (pBlob) ;
}
/b> Уу Глава 7. Проверка попадания
Координаты точки попадания приводятся к мировым координатам. Мы создаем новое пятно, задаем его положение и присоединяем к текущей фигуре. Обратите внимание на то, что новый объект (пятно) присоединяется к списку фигур, тем самым мы обеспечиваем его удаление при уничтожении всего макета. Помните, что для правильной работы проверки попаданий нельзя удалять использованные объекты C++.
Предлагаю выполнить небольшое упражнение. Посмотрите на исходный текст функции AddBlob. Действительно ли необходимо приводить точку попадания к мировым координатам? Можно ли добиться того же результата, не выполняя этого преобразования? Попробуйте модифицировать программу и посмотрите, будет ли она работать.
Итоги
Мы узнали, как выделять объекты, щелкая мышью в окне, как определить выделенную грань и положение точки попадания в объекте. Теперь у нас есть все необходимые инструменты для выделения трехмерных объектов и работы с ними. Если вы не следите за моими описаниями, я снова советую запустить отладчик и посмотреть, как происходит обработка сообщений мыши.
Расставляем декорации
Глава 2 Расставляем декорации
Структура приложения

Основные принципы архитектуры, выбираемые в начале проекта, нередко оказывают значительное влияние на его развитие. Неудачная структура может привести к тому, что ваш проект станет «обрастать бородавками» быстрее, чем вы будете их удалять. Например, при написании книги «Animation Techniques for Win32» я еще не обладал достаточным опытом программирования на C++ и работы с Microsoft Visual C++ и библиотеками MFC. В начале работы над примерами я совершил то, что сейчас считаю своей грубой ошибкой: воспользовался Visual C++ для построения однодокументного (SDI) приложения и решил, что мне удастся как-нибудь приспособить его для своих целей. Я сделал это лишь потому, что на тот момент приходилось выбирать между однодокументным и многодокументным (MDI) типами приложения, а MDI-приложение явно не подходило для воспроизведения игровой анимации. Сейчас я ясно понимаю, что мог бы существенно упростить все свои примеры, если бы отказался от принятой в Visual C++ метафоры «документ/вид» и воспользовался простым окном с меню.
На этот раз я решил, что структура моих приложений-примеров должна быть проще и ближе к той, которая может понадобиться при разработке компьютерной игры (это вовсе не означает, что она не годится для более серьезных целей — просто я отказался от использования метафоры «документ/вид» для упрощения программы).
В сущности, как мы вскоре убедимся, используемый нами оконный объект может выступать в роли главного окна приложения, как это было в примере
Структура приложения 'Чр!' 33
Basic, или в роли дочернего окна, как в приложении Stage. Можно даже переключиться в полноэкранный исключительный режим, взять на себя все управление экраном и установить другой видеорежим вместо того, в котором находилась Microsoft Windows перед началом работы приложения. Хотя подобная структура приложения значительно проще той, которую я использовал раньше, она оказывается достаточно гибкой и подходит для самых разных целей.
Я не предлагаю вам создавать реальные программы на основе нашего примера. Тем не менее он может пригодиться для экспериментов с новыми идеями. Библиотека 3dPlus проектировалась для обучения, а не для создания коммерческих продуктов. Если вы захотите применить ее при реальной разработке, придется добавить немалый объем кода для обработки ошибок, исключений и т. д.
Для построения базовой структуры приложения в Visual C++ следует выполнить следующие действия:
1. Воспользуйтесь Visual C++ MFC AppWizard для создания однодокументного приложения, в котором отключена поддержка баз данных, поддержка OLE и вывода на печать. В результате получается самое простое оконное приложение, создаваемое с помощью AppWizard. Я назвал свой проект Stage. Вы можете выбрать как статическую компоновку библиотек MFC, так и динамическую, с использованием DLL. Во всех своих примерах я пользовался DLL, чтобы сократить размер ЕХЕ-файла.
2. Исключите из проекта файлы классов документа и вида. В моем случае это были файлы StageDoc.h, StageDoc.cpp, StageView.h и StageView.cpp. Удалите эти файлы из каталога проекта. У вас остаются три программных файла на C++: Stage.cpp, MainFrm.cpp и StdAfx.cpp.
3. Отредактируйте исходные файлы и исключите из них любые ссылки на заголовочные 41айлы классов документа или вида.
4. Вставьте в файл StdAfx.h директивы для включения файлов •^mmsystem.t^ и <d3drmwin.h>. Первый из них используется функциями для работы с джойстиком, которые понадобятся нам позднее, а во втором определяются все функции Direct3D.
5. Включите файл <3dplus.h> в StdAfx.h или Stage.h. Я включил его в Stage.h, чтобы при внесении изменений в библиотеку мне не приходилось бы заново строить предварительно компилированный заголовочный файл в приложении, с которым я работаю.
6. В окне диалога Project Settings (команда Build ¦ Settings) поместите библиотеки Direct3D и 3dPlus в список Link. Во все мои примеры включались файлы SdPlusd.lib, d3drm40f.lib, ddraw.lib и winmm.lib. Обратите внимание: проект библиотеки 3dPlus позволяет работать как с отладочной OdPlusd.lib), так и с окончательной версией библиотеки OdPlusd.lib). В своих примерах я пользовался отладочной версией 3dPlus, чтобы вы могли просмотреть все символы, входящие в библиотеку, а при желании — трассировать ее модули. Библиотека d3drm содержит все трехмерные функции, вызываемые в примере. Библиотека ddraw обеспечивает работу DirectDraw, a winmm — ряд мультимедиа-функций для воспроизведения звука.
Подготовка завершена. Нам еще предстоит добавить в наше приложение довольно много программного кода перед тем, как его можно будет откомпилировать и построить, однако делать это придется уже без помощи AppWizard. На Рисунок 2-1 показана структура приложения Stage.
34 1У Глава 2. Расставляем декорации
Рисунок. 2-1. Структура приложения

Блок с пометкой Механизм визуализации Direct3D чем-то напоминает Рим — все дороги ведут к нему. Мы рассмотрим каждый из этих блоков, когда будем описывать процесс взаимодействия классов семейства C3d с механизмом визуализации Direct3D.
Отображение главного окна
Далее необходимо изменить инициализирующий код приложения, чтобы обеспечить создание главного окна. Для этого следует отредактировать функцию CStage::lnitlnstance в файле Stage.cpp. Когда AppWizard строит базовое приложение SDI, он включает в функцию Initlnstance код для создания пустого документа, который, в свою очередь, создает главное окно. Поскольку мы удалили код, относящийся к документу, придется строить главное окно самостоятельно. Новая версия функции Initlnstance выглядит следующим образом:
BOOL CStageApp::Initlnstance()
{
// Стандартная инициализация
// Если вы не используете какие-либо возможности и желаете // сократить размер итогового выполняемого файла, следует // вручную удалить ненужные процедуры инициализации.
#ifdef _AFXDLL
Enable3dControls(); // Вызывается при использовании MFC //в виде совместной DLL-библиотеки
#else
Enable3dControlsStatic(); // Вызывается при статической
// компоновке MFC ttendif
LoadStdProfileSettings();// Загрузить стандартные параметры
// из INI-файла (включая MRU) // Загрузить главное обрамленное окно CMainFrame* pFrame = new CMainFrame;
if (!pFrame->LoadFrame(IDR_MAINFRAME,
35
Отображение главного окна
WSJ3VERLAPPEDWINDOW WS VISIBLE)) {
return FALSE;
}
// Сохранить указатель на главное окно
m pMainWnd = pFrame;
return TRUE;
}
Обратите внимание на два важных действия: вызов функции LoadFrame для загрузки и отображения обрамленного окна и сохранение указателя на него в переменной m_pMainWnd. Указатель сохраняется для того, чтобы классы MFC могли передавать сообщения главному окну приложения, тем самым обеспечивая его правильную работу. Кроме того, необходимо отредактировать файл MainFrm.h и объявить конструктор CMainFrame открытым (public) — по умолчанию он является защищенным (protected). Заодно включите в перечень открытых членов CMainFrame объявление переменной C3dWnd m_wnd3d.
Если на этой стадии откомпилировать и запустить программу, на экране появится главное окно с меню и панелью инструментов. Давайте продолжим работу и закончим программу Stage, cpp, чтобы можно было перейти к созданию трехмерного окна.
В файл Stage.cpp осталось добавить две важные функции: Onldle и OpenDocumentFile. Первая из них обновляет изображение в окне во время пассивной работы приложения, а вторая необходима для правильного открытия файлов. Воспользуйтесь ClassWizard и включите в класс CStageApp функцию Onldle, затем отредактируйте ее и приведите к следующему виду:
BOOL CStageApp::Onldle(LONG ICount) {
BOOL ЬМоге = CWinApp::Onldle(ICount);
// Получить указатель на главное обрамленное окно CMainFrame* pFrame = (CMainFrame*) m_pMainWnd;
if (pFrame) (
// Обновить изображение в трехмерном окне
if (pFrame->m_wnd3d.Update(1)) { ЬМоге = TRUE;
} ! return ЬМоге;
}
Функция Onldle вызывается во время периода пассивности приложения. Основной принцип ее работы заключается в том, что, когда нашему приложению нечего делать, функция возвращает FALSE, а управление передается другому приложению. Если же оно должно выполнять полезные действия (скажем, приводить в движение трехмерный макет), возвращается значение TRUE, свидетель-
36 iii^1' Глава 2. Расставляем декорации
ствующее о необходимости выделения дополнительных квантов пассивного времени. Функция C3dWnd::Update, вызываемая из Onldle, возвращает значение TRUE в том случае, если отображаемые объекты существуют, и FALSE, если их нет. При таком подходе наше приложение не станет зря требовать дополнительные кванты в том случае, когда ему нечего рисовать.
Вторая функция, которую необходимо включить в Stage.cpp, OpenDocumentFile, предназначена для работы со списком последних открывавшихся 41айлов в меню. Если добавить в программу код, приведенный в следующем разделе («Модификация главного окна»), но не включить эту функцию, то все будет нормально до тех пор, пока вы не щелкнете на каком-либо имени файла в нижней части меню. В этот момент MFC выдает ASSERT, а ваше приложение останавливается. Жаль, конечно, что работа MFC так тесно привязана к архитектуре «документ/вид», но здесь уж ничего не поделаешь, и нам придется решать те проблемы, которые возникли в тот момент, когда мы удалили из своего проекта 4'>айлы Doc и View и тем самым вмешались в работу AppWizard. К счастью, сделать это несложно. Все, что необходимо, — переопределить функцию CWinApp::OpenDocumentFile (включите эту функцию в класс CStageApp с помощью ClassWizard):
CDocument* CStageApp::OpenDocumentFile(LPCTSTR
IpszFileName)
{
// Функция вызывается при выборе пользователем // строки из меню последних открывавшихся файлоь. // Конкретное возвращаемое значение неважно, оно лишь // должно отличаться от NULL при успешном выполнении // и быть равным NULL при неудаче.
CMainFrame* pFrame = (CMainFrame*) m_pMainWnd;
if (pFrame) {
return (CDocument*) pFrame->OpenFile(IpszFileName);
} else {
return NULL;
} }
Если пользователь щелкнул на имени файла в меню, необходимо передать выбранное имя главному обрамленному окну для обработки, словно пользователь выполнил команду Open в меню File.
Вот и все, что касается общей структуры приложения, однако мы еще не занимались реализацией конкретных функций (таких, как OpenFile), так что при попытке откомпилировать программу вы получите несколько ошибок. Сейчас мы настроим параметры главного окна и добавим в него трехмерные объекты.
Модификация главного окна
Для того чтобы главное окно приложения выглядело и работало так, как мы желаем, нам предстоит изрядно потрудиться. При этом нам придется заниматься множеством мелких подробностей, однако я рассмотрю их все — если вы не относитесь к числу экспертов по MFC, то сможете лучше представить себе, как
Модификация главного окна '^ИЯ 37
работает эта библиотека. После этого мы оставим в покое структурный код и сосредоточим свои усилия на более интересных аспектах, связанных с отображением трехмерных объектов (самое время налить себе очередную чашку кофе, как это только что сделал я).
Создание трехмерного окна
AppWizard включает в функцию OnCreate класса CMainFrame довольно много кода, предназначенного для создания самого окна, панели инструментов и строки состояния. Нам придется добавить специальный фрагмент, в котором трехмерное окно будет создаваться как потомок главного обрамленного окна. Заодно мы создадим исходный макет с трехмерным объектом — по крайней мере, мы сможем проверить, работает ли наша программа. Одно их худших разочарований в жизни программиста — ввести несколько сотен строк программы, откомпилировать и запустить ее лишь для того, чтобы увидеть большое черное окно (вряд ли кто-нибудь при этом станет прыгать от радости). Я привожу текст 41ункции OnCreate за исключением фрагментов, сгенерированных AppWizard, чтобы вы могли увидеть, что же именно мы добавили в нее (полный текст функции находится в проекте Stage на прилагаемом к книге CD-ROM):
int CMainFrame::OnCreate(LPCREATESTRUCT IpCreateStruct) (
// Создать трехмерное окно if (!m_wnd3d.Create(this, IDC_3DWND)) ( return -1;
}
NewScene () ;
ASSERT(m_pScene) ;
// Создать трехмерный объект C3dShape shi;
shi.CreateCube(2) ;
m_pScene->AddChild(&shl) ;
shl.SetRotation(l, 1, 1, 0.02);
return 0;
}
Этот фрагмент во многом напоминает тот, который использовался в программе Basic для отображения исходного макета. Обратите внимание на то, что константа IDC_3DWND включается в проект командой View] Resource Symbols в меню Visual C++. Класс CMainFrame пополнился двумя членами: m_wnd3d и m_pScene. Переменная m_wnd3d была включена нами в MainFrm.h ранее, после редактирования функции CStageApp::lnitlnstance (стр. 35). Переменная m_pScene добавляется следующим образом:
38 ¦¦У Глава 2. Расставляем декорации
class CMainFrame : public CFrameWnd
public:
C3dWnd m_wnd3d;
CSdScene* m_pScene;
};
ПРИМЕЧАНИЕ
Блюстители чистоты C++ могут неодобрительно отнестись к тому, что объекты окна и макета были объявлены мной как открытые. Тем не менее я часто поступаю так в своих примерах, чтобы не возиться со специальными функциями доступа (например, GetScene). Прямой доступ к объектам позволяет получить более компактный код, даже если при этом нарушается принцип инкапсуляции.
Теперь в нашем главном окне содержится трехмерное окно и указатель на текущий макет. Возвращаясь к функции OnCreate на предыдущей странице, проследим за последовательностью действий: сначала мы создаем трехмерное окно, затем при помощи функции NewScene строим трехмерный макет (работа этой функции будет рассмотрена ниже), после чего мы создаем куб, присоединяем его к макету и начинаем вращать. Если взглянуть на текст функции C3dWnd::Create в библиотеке 3dPlus, нетрудно увидеть, что она создает трехмерное окно в качестве окна-потомка, а передаваемый при ее вызове указатель this (см. предыдущую страницу) используется для определения окна-родителя. Конечно, достижением программистской мысли это не назовешь, и все же данный факт достаточно важен для понимания основ.
Настройка размеров окна
На моем компьютере установлено разрешение экрана 1280х 1024. Microsoft Windows обладает одной скверной привычкой — по умолчанию она создает громадное окно лишь потому, что у меня установлено большое разрешение экрана. При работе с приложениями, для которых такое большое окно не требуется, я обычно устанавливаю исходный размер окна, включая пару лишних строк в CMainFrame::PreCreateWindow. В приведенном ниже фрагменте задается начальный размер окна 300х350 пикселей:
BOOL CMainFrame::PreCreateWindow(CREATESTRUCT& cs) {
// Задать исходный размер окна
cs.cx = 300;
cs.су = 350;
return CFrameWnd::PreCreateWindow(cs);
ЧЁЙЙ-Й*
Модификация главного окна "тЩЦ: 39
Функция NewScene
Настало время поближе познакомиться с функцией NewScene, о которой было сказано выше:
BOOL CMainFraitie : : NewScene ()
{
// Удалить макет, если он существует if (m pScene) {
m_wnd3d.SetScene(NULL) ;
delete m_pScene;
m_pScene = NULL;
}
// Создать исходный макет m_pScene = new CSdScene;
if (!m_pScene->Create()) return FALSE;
// Установить источники света C3dDirLight dl;
dl.Create(0.8, 0.8, 0.8);
m_pScene->AddChild(&dl) ;
dl.SetPosition(-2, 2, -5);
dl.SetDirectionfl, -1, 1);
m_pScene->SetAmbientLight(0.4, 0.4, 0.4);
m wnd3d.SetScene(m pScene);
return TRUE;
t
Мы включим функцию NewScene в файл MamFrm.cpp. Она удаляет существующий макет и создает новый, со стандартным расположением источников света. Затем макет присоединяется к сцене, которая является частью трехмерного окна. Экспериментируя с трехмерными объектами, я хочу быть уверенным в том, что они уничтожаются и создаются без всяких проблем. Данная функция позволяет удалить все созданные ранее объекты и заново начать работу со макетом (она принесла большую пользу, когда мой малолетний сын схватил джойстик и загнал все объекты куда-то за пределы экрана).
Пересчет размеров трехмерного окна
Так как AppWizard создал панель инструментов и строку состояния, занимающие место в клиентной области окна, нам необходимо иметь возможность заново вычислить размеры трехмерного окна в том случае, если пользователь перемещает или убирает панель инструментов или же скрывает строку состояния. Воспользуйтесь ClassWizard и создайте функцию CMainFrame::RecalcLayout, которая переопределяет функцию CFrameWnd::RecalcLayout:
void CMainFrame::RecalcLayout( BOOL bNotify) 40 iiy Глава 2. Расставляем декорации
\
/I Заново разместить служебные области
//и поместить трехмерное окно в центр.
// Размещение служебных областей выполняется
// обрамленным окном.
CFrameWnd::RecalcLayout(bNotify) ;
// Определить размеры свободного места //в клиентной области // для размещения трехмерного окна CRect re;
RepositionBars(О,
OxFFFF,
IDC_3DWND,
CWnd::reposQuery,
&rc) ;
if (IsWindow(m_wnd3d.GetSafeHwnd())) f m_wnd3d.MoveWindow(&rc, FALSE);
}
В сущности, данный фрагмент определяет размеры свободного места в клиент-ной области и использует его для размещения трехмерного окна. Более подробные объяснения можно найти в документации по MFC.
Уничтожение окна
Все хорошее когда-нибудь приходит к концу — в том числе и окна. Включая в программу функцию OnDestroy, мы сможем освободить память, занятую нашими объектами (для этого следует вызвать ClassWizard и указать обрабатываемое сообщение WM_DESTROY):
void CMainFrame::OnDestroy() {
CFrameWnd::OnDestroy() ;
// Уничтожить текущий макет m_wnd3d.SetScene(NULL) ;
if (m_pScene) { delete m_pScene;
}
Если при завершении программы не удалить объекты, созданные во время ее активности, это приведет к «утечке памяти». Благодаря механизму работы с памятью, который используется MFC в отладочных версиях программ, вы получите сообщение о таких «утечках» после завершения приложения, так что обнаружить их просто, а вот ликвидировать посложнее, так что давайте сразу будем программировать аккуратно.
Модификация главного окна '''^ 41
Подготовка к отображению трехмерного окна
Одна из самых интересных особенностей механизма визуализации DirectSD заключается в том, что он работает непосредственно с видеопамятью и не пользуется интерфейсом графических устройств Windows (GDI). Следовательно, крайне важно, чтобы механизм визуализации точно знал экранное положение того окна, с которым он работает. Если это положение будет указано неверно, то он либо не станет рисовать вообще, либо, что еще хуже, примется рисовать поверх других окон. Кроме того, механизм визуализации должен знать, активно приложение или нет и получило ли оно какие-либо сообщения, связанные с палитрой. Если приложение переходит в фоновый режим, механизм визуализации должен освободить палитру, чтобы ей могли воспользоваться другие приложения. Все эти требования выполняются функциями, предназначенными для обработки сообщений WM_ACIVATEAPP, WM_PALETECHANGED и WM_MOVE:
void CMainFrame::OnActivateApp(BOOL bActive, HTASK hTask) {
CFrameWnd::OnActivateApp(bActive, hTask) ;
// Сообщить трехмерному окну об изменении состояния m_wnd3d.SendMessage(WM_ACTIVATEAPP, (WPARAM)bActive, (LPARAM)hTask) ;
}
void CMainFrame::OnPaletteChanged(CWnd* pFocusWnd) {
// Сообщить трехмерному окну об изменении палитры m_wnd3d.SendMessage(WM_PALETTECHANGED, pFocusWnd ?
(WPARAM)pFocusWnd->GetSafeHwnd() : 0);
\
void CMainFrame::OnMove(int x, int y) {
CFrameWnd::OnMove(x, y) ;
// Сообщить трехмерному окну о перемещении обрамленного
окна
m_wnd3d.SendMessage(WM_MOVE,
О,
MAKELPARAM(0, 0)) ;
Как видите, для нормальной работы DirectSD необходимо лишь, чтобы ваше приложение посылало сообщения трехмерному окну, которое берет на себя частные аспекты взаимодействия с механизмом визуализации.
42 'ЭДГ Глава 2. Расставляем декорации
Меню File
Остается лишь предусмотреть обработку команд меню File ¦ New и File ¦ Open. Ранее мы уже построили функцию для удаления текущего и создания нового макета, поэтому команда File ¦ New реализуется тривиально (воспользуйтесь ClassWizard для добавления идентификатора объекта ID_FILE_NEW):
void CMainFrame::OnFileNew()
{
NewScene ();
}
Команда File ¦ Open обрабатывается двумя следующими функциями:
BOOL CMainFrame::OpenFile(const char* pszPath) {
// Попытаться открыть файл с фигурой
C3dShape sh;
const char* pszFile = sh.Load(pszPath);
if (!pszFile) return FALSE;
// Создать новый макет NewScene ();
ASSERT(m pScene);
// Присоединить новую фигуру к макету m pScene->AddChild(&sh);
sh.SetRotation(l, 1, 1, 0.02);
// Включить имя в список последних открывавшихся файлов AfxGetApp()->AddToRecentFileList(pszFile) ;
return TRUE;
}
void CMainFrame::OnFileOpen() f
OpenFile(NULL) ;
}
Теперь давайте посмотрим, как работает функция OpenFile. Сначала мы создаем новый объект C3dShape и вызываем его функцию Load. Эта функция либо пытается открыть файл, либо, при отсутствии заданного имени файла, выводит окно диалога, в котором пользователю предлагается выбрать файл. В том случае, если файл имеет правильный формат, код класса C3dShape открывает его и создает трехмерный объект на основании данных из файла. Понятно, правда? Далее мы присоединяем новый объект к макету и приводим его во вращение, чтобы увидеть макет во всей красе. Имя файла заносится в список последних открывавшихся файлов, что облегчает его повторное открытие в будущем (вспомните, что функция OpenFile также вызывается в функции
Модификация главного окна 'vS 43
OpenDocumentFile в Stage.cpp, при выборе пользователем одного из файлов в меню).
Осталось добавить несколько завершающих штрихов, после которых проект Stage будет нормально компилироваться и работать. Прежде всего необходимо инициализировать переменную m_pScene в конструкторе CMainFrame, для этого следует включить в конструктор строку m_pScene = NULL. Кроме того, поскольку функции NewScene и OpenFile не были созданы с помощью ClassWizard, придется вручную добавить их объявления в конструктор CMainFrame в файле MainFrm.h.
Если вы еще не заснули, можете откомпилировать и скомпоновать проект. В вашем распоряжении появилась действующая программа для просмотра трехмерных объектов. Разумеется, вы пока не имеете ни малейшего представления о принципах ее работы, но мы рассмотрим их чуть позже, и они наверняка покажутся вам интереснее того, чем мы занимались до сих пор.
Окна, ракурсы и устройства
Термин окно обладает множеством значений. В традиционном графическом программировании он соответствует способу проектирования изображения на плоскую поверхность, а у многих из нас он вызовет ассоциации с объектами в знакомой операционной системе с громадным количеством разных API. Как бы лично вы ни понимали этот термин (я не собираюсь никого обижать), он неимоверно перегружен значениями и уступает в этом смысле разве что термину объект. Как бы тщательно я ни подбирал слова при описании механизма визуализации, кто-нибудь все равно не поймет меня или будет настаивать па том, что термин используется неверно. Лично я считаю, что любая общепринятая терминология, будь она трижды неверна, вполне подходит и для меня. То же самое относится и к документации. Если в ней что-то именуется «окном», то я не буду называть это «что-то» иначе. Следовательно, даже если вам не нравится мой подход к описанию механизма визуализации, моей вины в этом нет — термины выбирали другие.
Давайте начнем с самого начала. Окно — объект Microsoft Windows, который обрабатывает сообщения и отображается в приложениях. Ракурсом называется математическое описание того, как набор объектов в трехмерном пространстве отображается в окне. Устройством (device) называется программа, связанная с реальным устройством, отвечающим за работу видеосистемы на вашем компьютере. Чтобы создать трехмерный макет в приложении, необходимо иметь окно, ракурс и устройство. На самом деле с одним устройством может быть связано несколько ракурсов и несколько окон, однако мы построим систему с одним окном, одним ракурсом и одним устройством. Вы управляете работой окна; управление ракурсом и устройством осуществляет механизм визуализации.
GDI и DirectDraw
Давайте посмотрим, что же на самом деле происходит, когда мы открываем окно на рабочем столе Windows. На Рисунок 2-2 изображено окно, помещенное в произвольном месте рабочего стола.
Теперь спустимся на аппаратный уровень и посмотрим на карту памяти видеоадаптера (Рисунок 2-3).
44 lly Глава 2. Расставляем декорации
Окно
Рисунок. 2-3. Карта памяти видеоадаптера

Окна, ракурсы и устройства
Графический вывод в Windows

Например, для того чтобы нарисовать в окне прямоугольник, следует вызвать функцию Rectangle. GDI спрашивает драйвер видеоустройства, умеет ли тот рисовать прямоугольники; если не умеет, GDI «договаривается» с драйвером о каком-нибудь другом способе рисования прямоугольника (построение множества линий или чего-нибудь в этом роде). Затем драйвер устройства обращается к содержимому видеопамяти или, если нам повезло, пользуется аппаратными особенностями видеокарты для непосредственно рисования прямоугольника. Как вы думаете, быстро проходит этот процесс или медленно? Правильный ответ — не очень медленно, но и быстрым его никак не назовешь. Все дело в универсальности GDI, за которую приходится расплачиваться.
Разве не замечательно было бы обойти GDI и драйвер видеоустройства и напрямую работать с видеопамятью? Конечно, это будет гораздо быстрее, но тогда вам придется досконально изучить работу всех видеокарт на планете. Библиотека DirectDraw предлагает идеальный вариант — вы обращаетесь к драйверу видеоустройства с запросом на прямой доступ к видеопамяти, и если драйвер разрешит, вы сможете непосредственно изменять значения пикселей на экране. Если же драйвер не сможет предоставить прямого доступа к видеопамяти, он по крайней мере создаст иллюзию того, что вы работаете с ней, хотя часть работы при этом будет выполняться самим драйвером. Приложение может пользоваться
46 ^ЦУ Глава 2. Расставляем декорации
функциями GDI или функциями DirectDraw в зависимости от своих требований к производительности. При установке DirectDraw процесс графического вывода происходит в соответствии с Рисунок 2-5.
DirectDraw также позволяет выполнять операции пересылки битовых блоков (бит-блит, bitbit), по возможности реализуемые с помощью аппаратных средств видеокарты. Вызывая блитовые функции DirectDraw, вы получаете либо потрясающую производительность (при прямом использовании особенностей адаптера), либо просто великолепную (при прямом переносе данных в видеопамять посредством кода DirectDraw).
Графический вывод с использованием DirectDraw

DirectDraw обладает еще одной важнейшей особенностью. Посмотрите внимательнее на Рисунок 2-3 на стр. 45. Для хранения изображения на экране используется менее половины имеющейся видеопамяти, а весь остаток пропадает даром. Нельзя ли распорядиться им более разумно? Если видеокарта на Рисунок 2-3 обладает аппаратным блиттером (специальная система, предназначенная для выполнения блито-вых операций), то в свободной памяти можно хранить вспомогательные спрайты, текстуры и т. д. Аппаратный блиттер позволит напрямую переносить изображения из внеэкранной видеопамяти в активную. Вам уже не приходится тратить время на пересылку видеоданных по компьютерной шине данных, благодаря чему возрастает скорость графического вывода. DirectDraw управляет свободной видеопамятью и позволяет создавать в ней внеэкранные поверхности или использовать ее любым другим способом. Фрагмент свободной памяти можно даже выделить под вторичный буфер, размеры которого совпадают с буфером главного окна, и построить в нем следующий кадр анимации, после чего воспользоваться исключительно быстрой блитовой операцией для обновления содержимого активной видеопамяти и смены изображения.
Пересылка видеоданных
Чтобы понять, почему данные в пределах видеопамяти копируются значительно быстрее, чем из основной памяти, необходимо понимать, как работает аппаратная часть компьютера. На Рисунок 2-6 изображена упрощенная модель работы основных компонентов видеосистемы компьютера.
Видеопроцессор, работающий в тесном сочетании с видеопамятью, обладает высокой производительностью. Пересылка данных между различными участками видеопамяти производится исключительно по видеошине. Пересылка из основной
Окна, ракурсы и устройства ^1^' 47
Рисунок. 2-6. Примерная архитектура видеосистемы

памяти в видеопамять обычно происходит значительно медленнее, поскольку блок данных из основной памяти должен пройти по главной шине данных (которая уступает шине видеоданных по разрядности), а затем через интерфейс видеошины, попасть на видеошину и лишь затем — в видеопамять. При пересылке данных между двумя шинами необходимо синхронизировать работу главного процессора с видеопроцессором. На это уходит время, и до завершения пересылки главный процессор не может делать ничего другого. На самом деле я несколько упростил ситуацию, однако вы можете убедиться в том, что в пересылке данных в пределах видеопамяти участвует меньше аппаратных средств, и потому обычно она происходит быстрее.
На самом деле пересылку данных в видеопамяти можно ускорить и дальше. Если ваше приложение будет работать в полноэкранном исключительном режиме (full-screen exclusive mode), видеокарта сможет переключаться между двумя страницами видеопамяти, благодаря чему анимация достигает производительности, присущей разве что играм для DOS.
Так какое же отношение все сказанное имеет к механизму визуализации? Он должен очень быстро производить графический вывод (прямо в видеопамять или, еще предпочтительнее, с использованием аппаратных средств видеокарты для поддержки работы с трехмерной графикой). К тому времени, когда вы будете читать эту книгу, на рынке уже появятся видеокарты с аппаратным ускорением трехмерной графики, стоимость которых не будет превышать $200. Как же происходит пересылка данных в этих условиях? Механизм визуализации обращается к функциям промежуточного программного уровня (в данном случае — непосредственного режима Direct3D), который сообщает видеокарте о необходимости выполнить ряд примитивных операций по обсчету трехмерной графики. Если видеокарта не может справиться с подобной задачей, необходимые функции эмулируются с привлечением программных драйверов Direct3D. При наличии таких программных компонентов мы получаем новую модель (Рисунок 2-7), при которой любое приложение (не только механизм визуализации) сможет вызвать набор трехмерных функций, которые будут реализованы с максимальной производительностью.
Кто же выигрывает от всего этого? Конечно же, приложения. Отныне ваша программа может выбрать любой путь, который обеспечит ей необходимую производительность при работе под Windows.
48
Глава 2. Расставляем декорации
Рисунок. 2-7. Работа с трехмерной графикой с участием промежуточного уровня Direct3D

Создание устройства и ракурса в приложении Stage
Давайте рассмотрим, какое же место в этой схеме занимает устройство и ракурс. Устройством называется программный компонент механизма визуализации, работающий с промежуточным уровнем Direct3D (см. Рисунок 2-7), а ракурс определяет, каким образом устройство используется при выводе в область видеопамяти, соответствующую окну. Следовательно, единственное назначение создаваемого окна заключается в том, чтобы указать устройству область видеопамяти, с которой оно будет работать. При создании трехмерного окна мы одновременно создаем устройство и указываем, к какому участку видеопамяти оно будет обращаться. Сделать это можно несколькими способами, но мы рассмотрим лишь два из них.
Проще всего вызвать функцию, которая непосредственно создает устройство по логическому номеру (handle) окна. Это очень удобно, поскольку вам совершенно не приходится думать о том, как работает промежуточный уровень Direct3D — вы указываете логический номер окна, а механизм визуализации делает все остальное. Кроме того, можно воспользоваться функциями DirectDraw для выделения памяти под видеобуферы, а также функциями Direct3D для создания Z-буфера (Z-буфером называется специальный видеобуфер, содержащий информацию о «глубине» каждого пикселя изображения). Затем вся эта информация передается механизму визуализации, который и создает устройство.
Разумеется, создать устройство непосредственно по логическому номеру окна гораздо проще, чем возиться с поверхностями DirectDraw, — и все же я пошел вторым путем. В начале работы над библиотекой 3dPlus я действительно создавал устройство по логическому номеру окна. Потом на выходных я разошелся и решил «поиграть» с 4)ункциями DirectDraw. В результате у меня появился набор классов-оболочек для функций DirectDraw, так что создать устройство на основе поверхностей DirectDraw стало ничуть не сложнее, чем по логическому номеру окна. Вероятно, мои слова вас не убедили, поэтому я приведу фрагмент программы, в котором создается объект-сцена в трехмерном окне нашего проекта Stage:
Окна, ракурсы и устройства
49
BOOL C3dWnd::CreateStage()
// Инициализировать объект DirectDraw if (!m_pDD) {
m pDD = new CDirectDraw;
} if (!m_pDD->Create()) return FALSE;
// Установить экранный режим для окна if ( !m_pDD->SetWindowedMode (GetSafeHwnd () ,
m_iWidth,
m_iHeight)) { return FALSE;
}
// Создать объект Direct3D if (!m_pD3D) {
m_pD3D = new CDirect3D;
} if (!m_pD3D->Create(m_pDD)) return FALSE;
// Задать цветовую модель if (!m_pD3D->SetMode(m_ColorModel)) return FALSE;
// Создать сцену if (!m_pStage) {
m_pStage = new C3dStage;
} if (!m_pStage->Create(m_pD3D)) return FALSE;
// Присоединить текущий макет m pStage->SetScene(m_pScene);
return TRUE;
}
Первая половина функции C3dWnd::CreateStage посвящена созданию объектов DirectDraw и Direct3D, предоставляющих основу для рисования трехмерных объектов в окне. Затем мы выбираем оконный режим для объекта DirectDraw (в отличие от полноэкранного режима) и задаем монохромную цветовую модель MONO для объекта Direct3D (цветовые модели рассматриваются в главе 10). Несколько последних строк создают объект C3dStage по объекту DirectDraw и присоединяют текущий макет к сцене. В свою очередь, объект-сцена C3dStage содержит объекты C3dDevice (устройство) и C3dViewport (ракурс), которые отвечают за взаимодействие с компонентами DirectDraw и Direct3D. Кроме того, сцена содержит объект C3dCamera; мы рассмотрим его ниже. Функция, в которой происходит фактическое создание сцены по объекту Direct3D, выглядит следующим образом:
50 ВД!8' Глава 2. Расставляем декорации
BOOL C3dStage::Create(CDirect3D* pD3D)
{
// Удалить существующий макет SetScene(NULL) ;
// Создать новое устройство по поверхностям Direct3D if (!m_Device.Create(pD3D)) return FALSE;
// Задать качество m Device.SetQuality(m_Quality);
// Создать ракурс if (!m_Viewport.Create(&m_Device,
&m Camera,
0,~0,
m_Device.GetWidth(),
m_Device.GetHeight())) ( return FALSE;
}
return TRUE;
Как видите, приведенная выше функция сводится к построению объектов C3dDevice и CSdViewport. Чтобы создать устройство, мы вызываем соответствующую функцию Direct3D и передаем ей указатель на используемые компоненты DirectDraw:
BOOL C3dDevice::Create(CDirect3D* pD3D)
{
if (m_pIDevice) {
m_pIDevice->Release();
m_pI Device = NULL;
}
m_hr = the3dEngine.Get!nterface()->CreateDeviceFromD3D(
pD3D->GetD3DEngine(),
pD3D->GetD3DDevice (),
&m pIDevice) ;
if (FAILED(m_hr)) { return FALSE;
} ASSERT(m_plDevice) ;
return TRUE;
Если бы устройство создавалось по логическому номеру окна, а не по набору поверхностей DirectDraw, то вместо функции CreateDeviceFromDSD была бы вызвана функция CreateDeviceFromHWND.
Окна,.ракурсы и устройства "^ 51
Раз уж у меня имелась рабочая программа, в которой использовались поверхности, а не логический номер, я решил оставить все без изменений, в качестве примера. Если когда-нибудь вам захочется самостоятельно поэкспериментировать с механизмом визуализации вместо того, чтобы пользоваться 3dPlus, можно подумать о создании устройства по логическому номеру окна. Разумеется, при работе с классами библиотеки 3dPlus можно совершенно не интересоваться их внутренней реализацией и считать их чем-то вроде «черных ящиков». Тем не менее знакомство с основами работы библиотеки 3dPlus поможет при дальнейшем расширении ее функций.
Проекционная система
После завершения краткого экскурса в аппаратную область давайте займемся более абстрактными вещами и рассмотрим работу проекционной системы. Поскольку объекты могут находиться в произвольной точке трехмерного пространства, нам нужно как-то определить, что же будет видно в нашем окне. Говоря на языке фотографов, нам необходимо указать направление камеры и фокальное расстояние линз. Кроме того, ради повышения эффективности необходимо задать две отсекающих плоскости: переднюю и заднюю. Все, что находится дальше задней или ближе передней плоскости, не будет воспроизводиться на экране. Усеченная пирамида, изображенная на Рисунок 2-8, определяет границы видимой области.
Положение передней и задней отсекающих плоскостей задается функциями IRLViewport::SetFront и IRLViewport::SetBack. СОМ-интерфейс IRLViewport применяется для управления ракурсом. Величину угла камеры можно изменить функцией IRLViewport::SetField. При создании объекта C3dStage некоторым параметрам присваиваются начальные значения, а другие остаются как есть. Если вы посмотрите на реализацию класса C3dStage, то увидите, что в нем отсутствуют специальные функции для изменения параметров видимой области, поскольку стандартные значения хорошо подходят для наших примеров (хотя при желании
Рисунок. 2-8. Видимая область

52
Глава 2. Расставляем декорации
вы можете самостоятельно написать нужные функции, поэкспериментировать с различными углами камеры и т. д., но пока не стоит опережать события).
Чтобы точно определить положение трехмерного объекта на экране, необходимо применить к его вершинам преобразование, которое отображает трехмерные пространственные координаты на двумерные координаты окна. Преобразование координат осуществляется с помощью матрицы размеров 4х4, которая является суперпозицией отдельных преобразовании перспективы, масштабирования и переноса. В сущности, для получения двумерных координат вершины следует умножить вектор трехмерных координат на матрицу преобразования. Если вам захочется поближе познакомиться с теорией, я бы порекомендовал книгу «Computer Graphics Principles and Practice» (см. библиографию на стр. 333) или какой-нибудь другой учебник по компьютерной графике.
Однако на практике все оказывается несколько сложнее (а разве бывает иначе?). В главе 1 я упоминал о том, что для представления иерархии преобразований в механизме визуализации применяются фреймы. Присоединенные к фреймам объекты могут перемещаться (трансформироваться) по отношению к другим фреймам. Для вычисления двумерных координат любого заданного объекта необходимо совместить результаты преобразований всех 4>реймов, расположенных в иерархии выше данного объекта, и таким образом определить окончательное преобразование объекта.
ПРИМЕЧАНИЕ
Ради наглядности я позволил себе небольшую поэтическую вольность. Фрейм не следует считать физическим объектом вроде изображенного на Рисунок 2-9; это всего лишь преобразование, применяемое ко всем его потомкам. Соответственно, фрейм не имеет физических размеров или формы. Однако я нередко представляю себе фреймы в виде структур из трубок или соломинок, склеенных друг с другом. Это помогает мне представить взаимное перемещение фреймов, присоединенных к макету
Возникает впечатление, что для последовательного выполнения всех этих преобразований потребуется много времени и усилий — и это действительно так, если выполнять все ненужные преобразования. Однако механизм визуализации действует более разумно. Он сохраняет копию матрицы итогового преобразования каждого фрейма (полученную умножением матриц всех преобразований фрейма), и в том случае, если все фреймы, находящиеся в иерархии выше данного, остались без изменений, итоговое преобразование можно не пересчитывать. Следовательно, работа с фреймами не обязательно приводит к потере производительности. На практике, если в вашем макете присутствует несколько движущихся объектов, все равно придется как-то определять их положение. Использование иерархических фреймов для задания относительного положения этих объектов значительно повышает вероятность того, что вам не придется выполнять лишних вычислений. Мы подробнее рассмотрим преобразования в главе 5, так что если вы чувствуете себя слегка сбитым с толку, не теряйтесь — позднее я все объясню.
Объект C3dStage является корнем иерархического дерева фреймов в проекционной системе нашего приложения. Все остальные фреймы так или иначе являются потомками, присоединенными к фрейму сцены. Фрейм камеры и фрейм текущего макета присоединяются непосредственно к фрейму сцены. Все фреймы,
Проекционная система ''^Ц: 53
входящие в макет, являются потомками фрейма макета. Используя фреймы подобным образом, вы очень легко определяете положение камеры по отношению к макету. Кроме того, можно без труда перемещать камеру по макету, создавая иллюзию полета, или закрепить камеру на одном месте и перемещать весь макет (еще один способ изобразить полет).
При создании фрейма сцены камера находится перед сценой и направляется на ее центр. Другими словами, камера располагается в отрицательной области оси Z. На Рисунок 2-9 показано взаимное расположение фреймов камеры и сцены.
Мы еще вернемся к фреймам и их влиянию на положение объекта, когда будем подробнее рассматривать преобразования. А пока давайте рассмотрим, как происходит загрузка фигур из файлов.
Рисунок. 2-9. Фрейм камеры и фрейм сцены

Создание фигур
Последний фрагмент кода, добавленный нами в главное обрамленное окно на стр. 43, предназначался для загрузки объекта C3dShape из файла на диске и его включения в текущий макет. Фигуры будут подробно рассмотрены в главе 4, однако я хочу показать вам, что представляют собой объекты C3dShape, и показать, почему я сделал их именно такими.
DirectX 2 SDK позволяет создавать приложения, работающие с механизмом визуализации. Однако SDK не содержит ни отдельных программ, ни простых функций для создания фигур — предполагается, что у вас имеются собственные
54
Глава 2. Расставляем декорации
средства для построения трехмерных объектов, текстур и т. д. Тем не менее я рассмотрел другой сценарии. Я представил себе небольшую компанию, которая желает оценить механизм визуализации перед тем, как вкладывать средства в инструменты, необходимые для работы с графикой в крупном проекте. Но как можно экспериментировать, не имея возможности создать собственную фигуру? На самом деле SDK все же содержит функции для построения фигур: вы составляете список координат вершин и набор списков лицевых вершин, после чего вызываете функцию для создания фигуры. Я решил, что для неопытного пользователя такой уровень работы с фигурами покажется слишком низким, и потому включил в библиотеку 3dPlus функции для создания распространенных геометрических фигур — кубов, сфер, цилиндров и конусов. Кроме того, я добавил код, облегчающий использование растров (bitmaps) Windows в качестве текстур; на момент написания книги такая возможность отсутствовала в SDK. Но перед тем, как реализовывать все это, я нашел функцию для загрузки фигуры из файла с расширением .X. Поэтому моя начальная реализация класса CSdShape состояла буквально из одного конструктора и функции Load. Даже этот минимальный объем кода позволил мне получить трехмерные объекты для отображения в окне.
В документации по DirectX 2 SDK сказано, что к 4) рейму могут присоединяться визуальные элементы (один и более). Визуальным элементом (visual) называется фигура или текстура, отображаемая на экране. Визуальный элемент не имеет собственного положения; его необходимо присоединить к фрейму таким образом, чтобы при выполнении преобразования он появился в нужном месте окна. Простоты ради я реализовал объекты CSdShape так, что с каждым из них связан ровно один фрейм и один визуальный элемент. Наличие фрейма и визуального элемента позволяет определить положение объекта 3dShape и его геометрическую форму, благодаря чему он становится больше похож на реальный объект. Недостаток такой схемы заключается в том, что если в макет входят 23 совершенно одинаковых дерева, то для создания леса понадобится 23 фрейма и 23 визуальных элемента, а это не очень эффективно. Гораздо лучше было бы создать всего одну фигуру (визуальный элемент) и воспроизвести ее в 23 различных местах. Другими словами, мы бы присоединили один визуальный элемент к 23 разным фреймам и добились существенной экономии памяти за счет данных, необходимых для определения 22 оставшихся фигур.
На самом деле вы все же можете присоединить один и тот же визуальный элемент к нескольким фреймам, как мы увидим в главе 4 при рассмотрении кло-нирования фигур. Однако описанная выше простая схема, невзирая на некоторую неэффективность, в нашем случае работает вполне нормально.
Давайте посмотрим, как устроена функция C3dShape::Load. При этом я познакомлю вас с некоторыми подробностями реализации и на примере продемонстрирую работу с СОМ-интерфейсами механизма визуализации.
const char* CSdShape::Load(const char* pszFileName) {
static CString strFile;
if (!pszFileName ¦¦ !strlen(pszFileName)) {
// Вывести окно диалога File Open CFileDialog dig(TRUE,
Создание фигур '^1 55
NULL, NULL,
OFN_HIDEREADONLY, _3DOBJ_LOADFILTER, NULL) ;
if (dIg.DoModal() != IDOK) return NULL;
// Получить путь к файлу strFile = dlg.m_ofn.IpstrFile,'
} else (
strFile = pszFileName;
}
// Удалить любые существующие визуальные элементы New () ;
// Попытаться загрузить файл ASSERT(m_pIMeshBld) ;
m hr = m_pIMeshBld->Load((void*)(const char*)strFile,
NULL,
D3DRMLOAD_FROMFILE ¦ D3DRMLOAD_FIRST,
C3dLoadTextureCallback,
this) ;
if (FAILED(m_hr)) ( return NULL;
}
AttachVisual(m_pIMeshBld) ;
m strName = "File object: ";
m strName += pszFileName;
return strFile;
}
Функцию Load можно использовать двумя способами. Если вам известно имя открываемого файла, вызывайте ее следующим образом:
C3dShape shape;
shape.Load("egg.x") ;
Если же вы хотите просмотреть файлы и выбрать из них нужный, вызов функции будет выглядеть так:
C3dShape shape;
shape.Load(NULL);
56 lly Глава 2. Расставляем декорации
Если имя файла нс указано, появляется окно диалога, в котором строка-фильтр равна *.х, так что по умолчанию в окне диалога отображаются только те файлы, которые может открыть данная функция. После получения имени открываемого файла вызывается локальная функция New, удаляющая из объекта-фигуры любые существующие визуальные элементы. Поскольку я всегда стараюсь создавать объекты, подходящие для повторного использования, вы можете вызывать функцию Load для объекта 3dShape произвольное количество раз. Мне кажется, что это гораздо удобнее, чем создавать новый объект C++ каждый раз, когда мне захочется поиграть с очередной фигурой.
Истинное волшебство происходит в следующем фрагменте, и его следует рассмотреть поподробнее:
ASSERT(m_pIMeshBld) ;
m_hr = m_pIMeshBld->Load((void*)(const char*)strFile, NULL,
D3DRMLOAD_FROMFILE ¦ D3DRMLOAD_FIRST, C3dLoadTextureCallback, this) ;
if (FAILED(m_hr)) { return NOLL;
}
Сначала мы проверяем, не равно ли NULL значение указателя m_plMeshBld. Подобные директивы ASSERT довольно часто встречаются в коде библиотеки 3dPlus. Затем мы вызываем 4'>ункцию IRLMeshBuilder::Load, которая загружает файл и создает на его основе сетку (mesh). СОМ-интерфейс IRLMeshBuilder предназначен для создания и модификации сеток. Сеткой называется набор вершин и граней, определяющих форму объекта (на самом деле в сетку входит еще кое-что, но на данном этапе такого определения будет вполне достаточно). Данная функция, как и большинство других СОМ-функций, возвращает значение типа HRESULT, в котором передаются сведения о том, успешно ли была вызвана функция. Для проверки значения HRESULT и определения того, успешно ли завершилась данная функция, служат два макроса — SUCCEEDED и FAILED. Эти макросы определяются среди функций OLE и не являются специфичными для Direct3D. Я сделал своим правилом присваивать результаты всех обращений к СОМ-интерфейсам, производимых в библиотеке 3dPlus, переменной m_hr, которая присутствует в любом классе семейства C3d. Если при этом вызов завершается неудачно и функция класса возвращает FALSE, можно проанализировать переменную класса m_hr и выяснить причину ошибки. Подобная уловка не претендует на гениальность, но сильно помогает при отладке.
Переменная m_plMeshBld инициализируется при конструировании объекта C3dShape:
C3dShape::C3dShape() (
m_pIVisual = NULL;
C3dFrame::Create(NULL) ;
ASSERT(m_pIFrame) ;
m_pIFrame->SetAppData((OLONG)this) ;
Создание фигур '"^l 57
m strName = «3D Shape»;
m^pIMeshBId = NULL;
the3dEngine.CreateMeshBuilder(&m_pIMeshBld);
ASSERT(m_pIMeshBld) ;
AttachVisual(m_pIMeshBld) ;
}
Глобальный объект the3dEngine пользуется некоторыми глобальными функциями Direct3D для создания различных интерфейсов трехмерной графики. Чтобы вы не подумали, будто я от вас что-то скрываю, покажу, откуда возникает интерфейс IRLMeshBuilder:
BOOL C3dEngine::CreateMeshBuilder(IDirect3DRMMeshBuilder**
pIBId)
(
ASSERT(m_pIWRL) ;
ASSER'. 'oIBId) ;
m_hr = m_pIWRL->CreateMeshBuilder(pIBld) ;
if (FAILED(m_hr)) return FALSE;
ASSERT(*pIBld);
return TRUE;
Пока я не стану объяснять, откуда берется значение m_plWRL, но вы наверняка уловили общий принцип: обращения к СОМ-интерфейсам мало чем отличаются от вызовов функций объектов в C++. Сходство настолько велико, что я использую префикс р1 для СОМ-интерфейсов. Чтобы понять отличия между ними, давайте посмотрим, что происходит с указателями на СОМ-интерфейсы при уничтожении объекта C3dShape:
C3dShape : : --C3dShape () {
if (m_pIVisual) m_pIVisual->Release() ;
if (m_pIMeshBld) m_pIMeshBld->Release();
m ImgList.DeieteAll () ;
Как видите, наши действия сильно отличаются от обычного удаления объектов по указателям. Завершая работу с СОМ-интерфейсом, вы обязаны вызвать его функцию Release, чтобы уменьшить значение его счетчика обращений. Если не сделать этого, то СОМ-объект будет жить в памяти вечно.
Напоследок я бы хотел сделать одно замечание, относящееся к вызову функций из конструкторов объектов C++. Как нетрудно догадаться, попытка создать интерфейс внутри конструктора может кончиться неудачей — чаще всего это происходит из-за нехватки памяти. В своей программе я даже не пытаюсь обнаружить такую ситуацию. Проблемы с памятью вызывают исключение, которое, как я надеюсь, будет перехвачено в вашей программе! Конечно, с моей стороны
58 1ЦУ Глава 2. Расставляем декорации
нехорошо перекладывать свою работу на других, однако создание мощной функциональной программы существенно увеличит ее объем, а я стараюсь по возможности упростить свой код, чтобы вам было проще разобраться с ним. Я уже упоминал во вступлении о том, что моя библиотека — не коммерческий продукт, а всего лишь набор примеров. Разработку коммерческой версии я оставляю вам. Если вы хотите научиться создавать мощные классы, которые должным образом обрабатывают исключения, я сильно рекомендую обратиться к книге Скотта Мей-ерса (Scott Meyers) «More Effective C+++: Thirty-Five More Ways to Improve Your Programs and Design» (Addison-Wesley, 1996).
Что же мы узнали в этой главе?
Мы увидели, как устроена базовая структура приложения, которым мы будем пользоваться во всей оставшейся части книги. Кроме того, мы узнали, для чего предназначена библиотека DirectDraw и как трехмерные объекты проектируются на плоский экран. Напоследок мы рассмотрели загрузку трехмерного объекта из файла .X и его отображение в текущем макете. Попутно я познакомил вас с некоторыми принципами функционирования графических библиотек. Если вы захотите получить более подробную информацию о работе библиотек, обращайтесь к документации по DirectX 2.
Разработка большей части примеров в оставшейся части книги начинается с копирования приложения Stage, и вы также можете воспользоваться этим путем. Скопируйте приложение, уберите из него все ненужное — и вы готовы к созданию своего первого макета.
Если вам кажется, что мы проделали в этой главе большую и сложную работу, послушайте короткую историю о том, что произошло со мной на данной стадии экспериментов.
После написания программы-примера для этой главы я смотрел на экран и восхищался своей работой. В кабинет зашла моя 8-летняя дочь. Ее отношение к моим достижениям оказалось не совсем таким, как я ожидал. Она спросила:
«Папа, а зачем там вертится чайник?» Я не знал, что ответить. Тем не менее у меня появился повод подумать о том, как много предстоит сделать, если я хочу создать что-нибудь мало-мальски впечатляющее.
Не беспокойтесь, дальше все пойдет легче.
Создание фигур
Глава 4 Создание фигур
Геометрия

Простите меня. Я знаю, что на обложке книги ни слова не сказано о том, что вам придется заниматься геометрией, но перед тем, как создавать собственные фигуры, необходимо познакомиться с терминологией и посмотреть, какие законы действуют в трехмерном мире. Для начала еще раз взглянем на систему координат.
В механизме визуализации используется левосторонняя система координат (разумеется, проницательный читатель поднимает левую руку и вертит пальцами, показывая, куда направлены оси х, у и z). Если же вы проспали весь разговор о системах координат в главе 1, посмотрите на Рисунок 4-1 — на нем изображена левосторонняя система, которой мы будем пользоваться.
Рисунок. 4-1. Левосторонняя система координат

Геометрия ^¦ 89
Положительная часть оси у направлена вверх, х — вправо, a z — в глубь экрана, от пользователя.
Разобравшись с направлениями осей, следует договориться о единицах измерения для создаваемых объектов. Единицы измерения — понятие условное. Например, можно измерять размеры создаваемых объектов в километрах. Возможно, это звучит нелепо, но если отодвинуть камеру на несколько километров от таких гигантских объектов, вид будет вполне нормальным — в нашем трехмерном мире нет загрязнения воздуха, которое бы могло испортить картину.
Давайте ненадолго отвлечемся от темы. Знаете ли вы, что одна из проблем, возникавших у астронавтов при выходе в космос, как раз и заключалась в том, что им не удавалось нормально оценить размеры объектов и расстояния до них? Дело в том, что интенсивность света, проходящего через космический вакуум, остается постоянной (тогда как в земной атмосфере свет рассеивается). Следовательно, объекты в космосе выглядят исключительно четко, даже если они удалены от вас на многие километры. Интересно, правда? Так и хочется обратиться в NASA и записаться на курсы астронавтов.
Аналогичнее проблемы возникают и с нашими фигурами, поскольку их размер на экране зависит только от размеров объектов и их расстояния от камеры. Остается лишь произвольно задать положение камеры и по нему определить, какими должны быть размеры объектов. В создаваемых нами макетах камера по умолчанию находится в 10 единицах от начала координат, то есть в точке с координатами О, О, -10. Объект размером в 1 единицу (скажем, куб с единичным ребром), находящийся в начале координат (О, О, 0), при стандартном расположении камеры смотрится на экране вполне нормально. Следовательно, длина, ширина и высота создаваемых нами объектов обычно должна составлять несколько единиц.
Поскольку мы пользуемся координатами с плавающей точкой, работа с численно малыми единицами не приведет к потере точности. Ситуация в корне отличается от манипуляций с целыми числами, которые нельзя бесконечно делить на меньшие части. На Рисунок 4-2 снова изображены оси, но на этот раз на них нанесены примерные значения координат, которыми мы будем пользоваться.
Рисунок. 4-2. Оси координат в типичном масштабе

Зная, куда направлены оси и где находятся наши объекты, можно приступать к созданию точек, определяющих внешний вид объекта.
90
Глава 4. Создание фигур
Одна вершина, две вершины, получается собачка
Давайте нарисуем собачку. Возьмите карандаш и соедините точки на Рисунок 4-3, начиная с точки 1 и следуя по порядку чисел.
Рисунок. 4-3. Соедините точки

— Папа, что ты делаешь?
— Изучаю работу механизма визуализации для компьютерной трехмерной графики.
— Как просто — я так тоже могу.
У нас получилась плоская, двумерная собака, но вы наверняка уловили общий принцип: указывая, в каком порядке следует соединять точки, можно определить довольно сложную фигуру. В геометрии такие точки называются вершинами, и в дальнейшем мы будем именовать их именно так. Вершина является точкой пересечения нескольких отрезков, причем нас будут интересовать только прямые отрезки (я уверен, что вы соединили точки на рисунке плавными кривыми; если же вы соединяли их отрезками прямых, то вы наверняка прославитесь в мире компьютерной графики, но про рисование собак вам лучше забыть). Разумеется, если картинка будет состоять из очень большого количества точек, то даже истинный нерд, соединяя точки по линейке, нарисует вполне приличную собаку.
Так в чем же суть всех наших рассуждений о собаках и точках? Дело в том, что компьютер умеет рисовать только прямые линии. Если мы захотим создать криволинейную фигуру, придется либо составлять ее из множества вершин, либо изобретать какой-нибудь другой способ для улучшения ее внешнего вида. Мы еще вернемся к рисованию криволинейных фигур в разделе «Создание твердых тел» на стр. 101. А пока достаточно запомнить на будущее определение вершин.
Геометрия ^^ 91
Векторы
Для определения вектора в трехмерном пространстве необходимо указать три координаты: х, у и z. Началом координат нашей системы является точка О, О, О. Рассмотрим точку в левом верхнем углу (и немного в глубь экрана), которая имеет координаты -2, 3, 4. Чтобы определить положение вершины, можно задать вектор, направленный из начала координат в точку трехмерного пространства. На Рисунок 4-4 изображен вектор, который определяет точку с координатами -2, 3, 4.
Рисунок. 4-4. Вектор, определяющий точку -2, 3, 4

Кроме того, с помощью вектора можно определить направление. Например, вектор О, 1, 0 определяет верхнее, то есть положительное направление оси Y (Рисунок 4-5).
В тех случаях, когда вектор используется для определения направления, его длина не имеет значения. Если хотя бы одна из координат вектора отлична от нуля, такой вектор однозначно задает направление. Тем не менее для определения направлений принято пользоваться единичными векторами. Длина единичного вектора равна 1, то есть:
x^+z2 = 1
При написании программы часто бывает нежелательно вычислять точные значения координат, при которых данный вектор становится единичным, поэтому обычно существует какое-нибудь средство для нормирования векторов (то есть приведения их к единичной длине). Класс C3dVector содержит функцию Normalize, которая выполняет эту задачу. Почему желательно задавать направление единич-
92
Глава 4. Создание фигур
Рисунок. 4-5. Вектор, определяющий направление

ным вектором? При изменении ориентации объекта, единичные векторы упрощают вычисления с вершинами объекта. Тем не менее, вызывая функции механизма визуализации, вы не обязаны передавать им единичные векторы, поскольку перед использованием вектора он автоматически нормируется. Необходимость нормирования возникает только при проведении ваших собственных вычислений с векторами (другое распространенное применение единичных векторов заключается в определении нормали к плоскости; см. раздел «Нормали» на стр. 95).
Но довольно о векторах. Давайте подведем итог: вектор может определять положение вершины или направление.
Ориентация
Для того чтобы однозначно задать положение и ориентацию трехмерного объекта в пространстве, необходимы три вектора. Первый вектор определяет положение объекта (или, по крайней мере, некоторой эталонной точки объекта). Второй вектор определяет направление, в котором обращен объект. Для чего же нужен третий вектор? На Рисунок 4-6 изображены три объекта, все они имеют одинаковую форму и обращены в одном направлении. Чем они отличаются друг от друга?
Отличие состоит в том, что все эти объекты повернуты на разный угол вокруг своей оси. Чтобы полностью задать ориентацию объекта, необходимо дополнительно определить направление, которое для объекта будет считаться верхним. На Рисунок 4-7 изображены верхние векторы для всех трех фигур.
Три вектора однозначно определяют позицию и ориентацию объекта.
Геометрия
93
Грани
В нарисованной вами собачке (Рисунок 4-3 на стр. 91) множество вершин использовалось для определения одной грани неправильной формы. Трехмерные объекты состоят из нескольких граней, причем для компьютера эти грани являются абсолютно плоскими. Чтобы изобразить «гладкую» сферу, потребуется довольно много плоских граней. Грани могут иметь любую форму — от простейших треугольников до сложных многоугольников, так что вам удастся собрать свой трехмерный объект из треугольников, квадратов, пятиугольников и вообще из любых фигур.
Рисунок. 4-6. Три объекта, обращенные в одном направлении

Для окончательного определения ориентации объекта необходимо задать верхние векторы

94
Глава 4. Создание фигур
Следует учесть, что независимо от заданной формы граней механизм визуализации во время рисования обычно разбивает многоугольные грани на треугольники. Конечно, если в вашем компьютере установлена какая-нибудь сверхмощная видеокарта вместе с такими же мощными драйверами, она может обойтись без деления и рисовать многоугольники непосредственно на аппаратном уровне. Вы спросите, какое это имеет значение? Если вы захотите построить свою фигуру из каких-нибудь особенных многоугольников, чтобы сократить количество граней и тем самым ускорить ее прорисовку, возможно, разумнее с самого начала собирать ее из треугольников или других многоугольников с более простой формой — все равно ваш компьютер воспроизводит грани как совокупности треугольников. Кроме того, иногда это может приводить к довольно неожиданным эффектам. Если просто задать вершины многоугольника и воспроизвести его в окне, ваш «плоский» многоугольник может обрасти треугольными выступами. Причины такого явления мы рассмотрим чуть позже, в разделе «Создание простых фигур» на стр. 97. А пока попробуем построить наши объекты из треугольников и квадратов и посмотрим, что получится.
Последнее, о чем следует помнить — при задании вершин, определяющих грань, необходимо перечислять их по часовой стрелке (Рисунок 4-8). Это очень важно, поскольку механизм визуализации воспроизводит только одну сторону грани. Ограничиваясь лишь передней поверхностью граней, механизм визуализации избавляется от необходимости рисовать невидимые грани и тем самым экономит время. Будьте внимательны при задании вершин грани и следите за тем, чтобы грань была видна с нужной стороны.
Рисунок. 4-8. Порядок обхода вершин грани

Разумеется, для создания нужной фигуры вершины граней также необходимо перечислять в правильном порядке. Нельзя наугад указать шесть-семь вершин и надеяться на то, что механизм визуализации как-нибудь соберет их в одну грань. Если в нашем примере вы не будете соединять точки по порядку, то получится не милая собачка, а сплошное безобразие.
Нормали
Нормалями называют людей, которые не станут заниматься геометрией ради собственного развлечения. Конечно, это шутка — например, я люблю геометрию, но при этом вполне нормален (я уверен в этом, потому что мне так говорили окружающие — честное слово!). Так что же такое нормаль?
Нормалью (по отношению к грани) называется вектор, определяющий ориентацию грани. На Рисунок 4-9 изображена грань вместе с нормалью к ней.
Геометрия '''^il 95
Рисунок. 4-9. Грань и нормаль

Нормалью грани является вектор, перпендикулярный ее поверхности. Для чего же нужны нормали? Знание ориентации граней может пригодиться при наложении текстур на объект. По нормалям можно определить, как следует ориентировать текстуру для достижения желаемого эффекта. На данный момент это несущественно, поэтому давайте рассмотрим другое применение нормалей.
В некоторых методиках трехмерного синтеза закраска грани зависит от направления ее нормали и расположения источников света в макете. Подобная закраска равномерно окрашивает грань и придает ей плоский вид. Поскольку большинство объектов в нашей жизни все же имеет объем, несколько плоских граней еще не дают иллюзии реальности. Любой художник покажет вам, как правильно наложенные тени на плоском листе бумаги создают иллюзию реального, твердого объекта. Следовательно, при разумном наложении теней на грани наших трехмерных объектов можно получить более реалистичные изображения. Именно здесь нужны нормали.
Механизм визуализации, с которым мы работаем, поддерживает несколько режимов закраски, однако для своих приложений я выбрал закраску методом Гуро (названную по фамилии автора). В этой методике закраска грани определяется положением нормалей в ее вершинах.
Предположим, у нас имеется прямоугольная грань и с каждой ее вершиной связан вектор нормали, как показано на Рисунок 4-10.
. Грань с нормалями вершин 96 ЯП' Глава 4. Создание фигур

На Рисунок 4-10 все нормали обращены вертикально вверх. При закраске по методу Гуро такая грань будет выглядеть плоской, так как все нормали вершин обращены в одном и том же направлении, и потому все точки грани, расположенные между вершинами, будут освещены одинаково. Возможно, это покажется вам неочевидным и даже непонятным, но давайте попробуем представить себе, что нормали определяют, насколько плоской выглядит грань у вершин. На Рисунок 4-10 все векторы направлены одинаково, поэтому вся грань выглядит плоской. Соответственно, ее освещенность остается постоянной.
Изменим положение нормалей и посмотрим, к" каким последствиям это приведет. На Рисунок 4-11 изображена та же самая грань с другими, неперпендикулярными нормалями*.
. Грань с неперпендикулярными нормалями

При освещении такая грань выглядит «вогнутой», поскольку направления нормалей изменяются от вершины к вершине так, что углы словно приподнимаются над плоскостью грани.
Если вы ничего не поняли, не огорчайтесь — сейчас мы продемонстрируем сказанное на примере программы, и тогда все станет гораздо понятнее.
Создание простых фигур
После небольшого экскурса в геометрию давайте займемся написанием программы, создающей несколько простых фигур. Данное приложение называется Shapes и находится в одноименном каталоге. Возможно, во время чтения стоит запустить приложение и посмотреть, как оно работает. На первый взгляд приложение Shapes ничем не отличается от Stage из главы 2, однако стоит щелкнуть в меню, как вы сразу увидите новые команды. Мы рассмотрим их назначение и реализацию. Весь интересующий нас код находится в файле MainFrm.cpp.
Начнем с исключительно простой фигуры — прямоугольника, который имеет четыре вершины, определяющие одну грань. Запустив приложение Shapes, вы найдете в меню Edit несколько команд с названиями фигур. Выберем команду Flat Face (то есть «плоская фигура»). Вот как выглядит ее программная реализация:
void CMainFrame::OnEditInsface() {
// Вставить простую плоскую грань
//и задать список вершин
D3DVECTOR vlist [] = (
На первый взгляд понятие «ненерпендикулярная нормаль» кажется внутренне протинорсчи-liliiM, однако если гопорить о нормалях к псршипам, а нс к граням, то ему можно придать смысл. — Иршчеч. пере».
Создание простых фигур <¦Ц 97
(-2, -2, -2},
t-2, -2, 2>,
{ 2, -2, 2},
{ 2, -2, -2} };
// Получить количество вершин в массиве
int nv = sizeof(vlist) / sizeof(D3DVECTOR);
// Определить вершины, входящие в каждую грань, // в формате:
// количество, вершина!, вершина2 и т. д. int flist [] = (4, О, 1, 2, 3, // 4 вершины, ...
О // Конец списка данных грани );
// Создать для фигуры новый макет NewScene ();
// Создать фигуру по списку вершин // и списку данных грани m pShape = new C3dShape;
m_p3hape-»Create (vlist, nv, flist);
// Присоединить фигуру к макету m_pScene-»AddChild(m_pShape) ;
}
Вершины грани содержатся в массиве векторов vlist. Каждый вектор определяет одну из четырех вершин, лежащих в плоскости у =-2. Прямоугольник имеет размеры 4х4 единицы. Первый вектор определяет ближнюю левую вершину, второй — дальнюю левую, третий — дальнюю правую и четвертый — ближнюю правую. Другими словами, мы обходим вершины по часовой стрелке.
Для определения фигуры используется целочисленный массив с информацией о грани, flist. Каждая грань в списке описывается количеством входящих в нее вершин, за которыми следует индекс каждой вершины в массиве vlist. Список граней завершается нулем. Он может содержать информацию о нескольких гранях, но в нашем случае определяется всего одна. Обратите внимание на то, что вершины пронумерованы в порядке О, 1, 2, 3, что соответствует их обходу по часовой стрелке, начиная с ближней левой, если смотреть на грань сверху. Поскольку грань находится в плоскости у =-2, она расположена ниже камеры (точки О, О, -10) и, следовательно, попадает в кадр.
Чтобы создать фигуру, следует вызвать функцию Create объекта C3dShape и передать ей в качестве аргументов список вершин, их общее количество и список данных грани. Не обращайте внимания на то, что происходит внутри объекта C3dShape, там нет ничего интересного — векторы и данные грани передаются в функцию механизма визуализации, которая и создает фигуру. Затем объект C3dShape присоединяется к макету, чтобы появиться в окне приложения. Если запустить приложение Shapes и выполнить команду Edit ¦ Flat Face, вы увидите что-нибудь похожее на Рисунок 4-12.
98 iy Глава 4. Создание фигур
Рисунок. 4-12. Приложение Shapes с одной плоской гранью

Обратите внимание на то, что грань выглядит плоской — это означает, что нормали ко всем вершинам имеют одинаковое направление. Вы можете проверить это командой View ¦ Normals, которая рисует возле каждой вершины небольшую стрелку, показывающую направление нормали. На Рисунок 4-13 изображена грань вместе с нормалями.
. Плоская грань с нормалями к вершинам

99
Создание простых фигур
Теперь давайте с теми же самыми данными создадим новую грань, но на этот раз укажем набор нормалей, направленных к центру грани. Ниже приведена функция для создания вогнутой грани, наподобие изображенной на Рисунок 4-11 на стр. 97:
void CMainFrame::OnEditDishface()
(
// Вогнутая грань D3DVECTOR vlist [] = (
(-2, -2, -2),
(-2, -2, 2),
( 2, -2, 2},
{ 2, -2, -2)
);
int nv = sizeof(vlist) / sizeof(D3DVECTOR);
D3DVECTOR nlist [] = {
( 1, 1, 1),
{ 1, 1, -1),
(-1, 1, -1),
{-1, 1, 1} };
int nn = sizeof(nlist) / sizeof(D3DVECTOR);
int flist [] = (4, О, О, 1, 1, 2, 2, 3, 3,
0 };
NewScene() ;
m_pShape = new C3dShape;
m_p3hape-»Create (vlist, nv, nlist, nn, flist);
m_pScene-»AddChild(m_pShape) ;
1
Как видите, мы пользуемся теми же самыми данными вершин, за исключением того, что к ним добавился еще один массив векторов, nlist. В этом массиве содержатся данные нормалей. Следует отметить, что векторы нормалей не являются единичными — их модули были взяты по моему усмотрению. Механизм визуализации нормирует эти векторы перед использованием.
Список данных грани (flist) изменился и теперь содержит количество вершин, за которым следуют пары индексов для вершин и нормалей. В этом случае используется другая версия функции Create объекта C3dShape, которая получает массивы вершин и нормалей, а также данные граней.
Результат выполнения этой функции изображен на Рисунок 4-14. Вы можете увидеть его на экране, для этого следует запустить приложение Shapes и выполнить команду Edit ¦ Dished Face.
Вы обратили внимание на то, что грань кажется вогнутой в середине? (Этот эффект особенно четко проявляется, если привести грань во вращение.) На случай, если вы забыли, напомню, что источник света находится в левом верхнем углу макета. С помощью приложения Shapes можно также убедиться в том, что
/b> lll^ Глава 4. Создание фигур
нормали, направленные за пределы грани, создают иллюзию выпуклости. Для того чтобы увидеть этот эффект, достаточно выполнить команду Edit ¦ Bulging Face.
Рисунок. 4-14. Грань с неперпендикулярными нормалями

Создание твердых тел
Довольно об отдельных гранях! Давайте немного изменим нашу программу и создадим куб:
void CMainFrame::OnEditDefcube() (
D3DVECTOR vlist [] = {
{-1, -1, -1),
{-1, -1, 1},
{ 1, -1, 1},
{ 1, -1, -1),
{-1, 1, -1),
{-1, 1, 1),
{ 1, 1, 1),
{ 1, 1, -1) };
int nv = sizeof(vlist) / sizeof(D3DVECTOR);
int flist [] = (4, 0, 3, 2, 1,
4, 3, 7, 6, 2,
4, 4, 5, 6, 7,
4, 0, 1, 5, 4,
4, 0, 4, 7, 3,
4, 2, 6, 5, 1,
n
Создание твердых тел
/b>
};
NewScene() ;
m_pShape = new C3dShape;
m_pShape-»Create (vlist, nv, flist) ;
m_pScene-»AddChild(m_pShape) ;
} .
Список вершин теперь состоит из восьми элементов, по одному для каждого из углов куба, а список граней содержит шесть элементов по числу граней куба. На Рисунок 4-15 изображен куб с пронумерованными вершинами, он поможет вам понять значения элементов списка данных граней в приведенном выше фрагменте. Следует помнить о том, что вершины каждой грани должны перечисляться по часовой стрелке относительно того направления, с которого будет видна данная грань.
Рисунок. 4-15. Нумерация вершин куба

Прежде, чем читать дальше, следует самостоятельно убедиться в том, что вы поняли смысл описания граней. Может, на это придется потратить немного времени, зато в дальнейшем вы не будете создавать невидимые поверхности, ориентированные в неверном направлении. Функция OnEditDefcube строит фигуру, изображенную на Рисунок 4-16. Чтобы увидеть куб на экране, выполните команду Edit] Default Cube.
Как вы думаете, почему закраска граней выглядит такой однородной? Выполните команду View ¦ Normals, и вы увидите, что нормали к вершинам куба обращены от углов, по направлению от центра куба. Поскольку мы не стали задавать свои нормали, механизм визуализации создал их по умолчанию, усредняя нормали всех граней, прилегающих к вершине. Подобное решение может показаться до-
/h2>
Глава 4. Создание фигур
Рисунок. 4-16. Вращающийся куб с принятым по умолчанию расположением нормалей

вольно странным, особенно при создании куба. Тем не менее оно выглядит вполне разумно при создании сферы или другой криволинейной фигуры, поскольку усредненные нормали помогают создать более реалистичный объект — закраска сглаживает края прилегающих граней.
Разумеется, мы все же рассчитывали увидеть другой куб, с плоскими гранями и четко различимыми ребрами. Для того чтобы решить эту проблему, достаточно определить свои собственные нормали. Для вершин каждой грани мы задаем нормали, направление которых совпадает с нормалью грани. Приведенная ниже функция создает куб с плоскими гранями:
void CMainFrame::OnEditFlatfacecube() {
D3DVECTOR vlist [] = {
(-1, -1, -1),
(-1, -1, 1),
( 1, -1, 1),
{ 1, -1, -1),
{-1, 1, -1),
{-1, 1, 1),
{ 1, 1, 1),
( 1, 1, -1} );
int nv = sizeof(vlist) / sizeof(D3DVECTOR);
D3DVECTOR nlist [] = { { i, 0, 0}, < 0, 1, 0), < 0, 0, 1), (-1, 0, 0),
Создание твердых тел
/h2>
{ 0, -1, 0), { 0, 0, -1}
);
int nn = sizeof(nlist) / sizeof(D3DVECTOR);
int flist [] = (4, 0, 4, 3, 4, 2, 4, 1, 4,
4, 3, 0, 7, 0, 6, 0, 2, 0, 4, 4, 1, 5, 1, 6, 1, 7, 1, 4, 0, 3, 1, 3, 5, 3, 4, 3, . 4, 0, 5, 4, 5, 7, 5, 3, 5, 4, 2, 2, 6, 2, 5, 2, 1, 2, 0
};
NewScene();
m_pShape = new C3dShape;
m_pShape-»Create (vlist, nv, nlist, nn, flist);
m_pScene-»AddChild(m_pShape) ;
t
Если запустить приложение и отобразить куб с плоскими гранями вместе с нормалями (сначала выполните команду Edit ¦ Flat-Faced Cube, затем — команду View ¦ Normals), вы увидите нечто похожее на Рисунок 4-17.
Рисунок. 4-17. Куб с плоскими гранями и векторами нормалей

Итак, теперь мы умеем создавать фигуры с плавными переходами граней (при которых нормали генерируются механизмом визуализации) или с более резкими переходами (при которых нормали задаются программистом). Иногда бывает нужно создать криволинейный объект, на котором присутствуют острые ребра. На Рисунок 4-18 изображен конус с закругленными сторонами и плоским основанием (команда Edit ¦ Cone).
/h2>
Глава 4. Создание фигур
Рисунок. 4-18. Конус

Если внимательно рассмотреть конус, можно заметить, что его боковая поверхность составлена из 16 треугольников, а основание имеет форму диска. Закраска боковых треугольников создает иллюзию криволинейной поверхности, а закраска основания придает ему плоский вид; между боковой поверхностью и основанием существует резко очерченная граница. Как добиться подобного эффекта?
Стороны конуса строятся точно так же, как и наш первый куб на стр. 101 — мы передаем механизму визуализации координаты вершин треугольников, образующих боковую поверхность, и он самостоятельно генерирует нормали, усредняя векторы нормалей для прилегающих граней. Это создает иллюзию кривизны боковой поверхности. Если бы мы просто включили основание конуса в список граней, использованных для создания боковой поверхности, то нормали для основания также были бы определены посредством усреднения нормалей основания и боковых граней. В результате нижняя грань казалась бы выпуклой, а граница между боковой поверхностью и основанием выглядела бы размытой.
Существуют два основных способа для получения плоского основания и резкой границы между основанием и боковой поверхностью. Самое простое, что можно сделать, — это внести основание в список граней с отдельным набором вершин. Разумеется, координаты этих вершин должны совпадать с координатами нижних сторон боковых граней, иначе в фигуре появятся «дырки». Задавая отдельные вершины для нижней грани, мы тем самым указываем, что нижняя грань не имеет прилегающих граней; когда механизм визуализации будет генерировать нормали для вершин основания, он просто использует для этой цели нормаль основания. Такой подход приводит к желаемому результату (плоскому основанию с резким переходом), однако он немного расточителен, поскольку нам приходится задавать лишний набор вершин (в данном случае — 16).
Более разумное решение состоит в том, чтобы использовать для основания конуса те же самые вершины, что и для боковых граней, но при этом задать для них нормали. Именно так работает функция, построившая конус на Рисунок 4-18. Ее преимущество заключается в том, что нам не придется задавать лишние вершины.
Создание твердых тел
/h2>
Конечно, хранение нормалей тоже потребует определенных расходов, однако все равно такой подход оказывается более экономичным, поскольку одна и та же нормаль используется для всех вершин основания. Пример программы приведен в следующем разделе, где мы рассматриваем тела вращения (такие, как конус).
Тела вращения
Тела вращения я впервые увидел в раннем детстве. Мой отец работал токарем, стоял целый день у токарного станка и точил фланцы, стержни, винты с нарезкой, трубы и т. д. (Рисунок 4-19). Токарный станок вращает металлическую заготовку, зажатую в патроне. К заготовке подносится резец, который срезает ненужный материал при вращении заготовки; положение резца определяет радиус детали. Продольное перемещение резца с одновременным вращением заготовки позволяет выточить стержень (гладкий или нарезной). Основная идея моего рассказа заключается в том, что твердый объект можно описать с помощью простой функции, определяющей радиус объекта в любой точке его длины.
Рисунок. 4-19. Токарный станок

Процесс построения тел вращения мало чем отличается от создания других трехмерных объектов. Необходимо задать набор вершин, определить, к каким граням они относятся, и затем при желании указать нормали. Поскольку тело вращения можно описать функцией зависимости радиуса от продольной координаты, нетрудно создать фрагмент программы, в котором такая функция используется для генерации вершин и данных граней. На Рисунок 4-20 изображено тело вращения, построенное именно этим способом. Чтобы увидеть тело вращения на экране, выполните команду Edit ¦ Solid of Revolution.
Ниже приводится фрагмент приложения Shapes, в котором создается изображенный на рисунке объект:
double RevolveFn(double z, void* pArg) (
if (z « -1.1) (
return sqrt(l — (z + 2)*(z + 2));
} else if (z » 0.8) (
/b> Щ^' Глава 4. Создание фигур
. Тело вращения

return sqrt(2 - (z - 2)*(z - 2));
} else (
return 0.5;
} }
// Создать тело вращения
void CMainFrame::OnEditSolidr()
{
// Создать объект по заданной функции
NewScene () ;
m_pShape = new C3dShape;
m_pShape-»CreateRSolid(-3.0, 2.2, 0.2, TRUE, TRUE, RevolveFn, NULL, 16);
m_pScene-»AddChiid(m_pShape) ;
// Развернуть объект, чтобы показать его со стороны m_pShape-»SetDirection(0, -1, 0) ;
)
Как видите, в данном случае мы имеем дело с двумя функциями. RevolveFn возвращает значения радиуса для заданной продольной координаты, а функция OnEditSolidr вызывается при выполнении команды меню Edit ¦ Solid of Revolution. Для построения объекта внутри функции OnEditSolidr вызываются функции RevolveFn и C3dShape::CreateRSolid. Аргументы CreateRSolid выглядят несколько необычно, поэтому позвольте мне объяснить их назначение.
Создавая функцию CreateRSolid, я не собирался делать ее универсальной. Вместо того чтобы обрабатывать координаты концов объекта, я решил всегда строить фигуру вдоль оси z. Таким образом, написанная вами функция (в данном
Тепа вращения
/h2>
случае RevolveFn) возвращает радиус объекта как функцию координаты по оси г. Аргументами CreateRSolid являются максимальное и минимальное значения координат по оси z, приращение по оси z, две логические величины, определяющие необходимость замыкания концов фигуры, указатель на функцию радиуса, необязательный аргумент, передаваемый в функцию радиуса, и наконец количество граней в круговой поверхности.
В нашем случае необязательный аргумент функции радиуса не используется, однако вы, например, можете передать в нем указатель на какую-нибудь таблицу данных. При таком подходе можно написать обобщенную функцию, которая строила бы более сложные тела вращения с использованием данных таблицы.
После того как объект будет создан, вам наверняка захочется развернуть его и переместить в итоговое положение. Как видно на примере функции OnEditSolidr в приведенном выше фрагменте, я развернул объект так, чтобы он был обращен вдоль оси у, а не вдоль своей первоначальной оси z.
Давайте посмотрим, как работает функция C3dShape::CreateRSolid. Приведенный ниже фрагмент взят из библиотеки 3dPlus:
// Создание тел вращения
BOOL CBdShape::CreateRSolid(double zl, double z2, double dz, BOOL bClosedl, BOOL bClosed2, SOLIDRFN pfnRad, void* pArg, int nFacets) (
New () ;
ASSERT(pfnRad) ;
ASSERT(dz != 0) ;
int iZSteps = (int)((z2 - zl) / dz);
if (iZSteps « 1) return FALSE;
int iRSteps = nFacets;
if (iRSteps « 8) iRSteps = 8;
double da = _twopi / iRSteps;
// Создать массив для вершин int iVertices °= (iZSteps + 1) * iRSteps;
D3DVECTOR* Vertices = new D3DVECTOR [iVertices];
D3DVECTOR* pv - Vertices;
// Создать массив для данных граней.
// Каждая грань имеет 4 вершины, за исключением торцов.
int iFaces = iZSteps * iRSteps;
int iFaceEntries = iFaces * 5 + 1;
if (bClosedl) iFaceEntries += iRSteps + 1;
if (bClosed2) iFaceEntries += iRSteps + 1;
int* FaceData = new int [iFaceEntries] ;
int* pfd = FaceData;
// Заполнить координаты вершин double z = zl;
/b> ¦¦¦¦1' Глава 4. Создание фигур
double r, a;
for (int iZ = 0; iZ «= iZSteps; iZ++) { r = pfnRadfz, pArg) ;
a = 0;
for (int iR = 0; iR « iRSteps; iR++) {
pv-»x = D3DVAL(r * sin(a));
pv-»y = D3DVAL(r * cos(a));
pv-»z = D3DVAL(z) ;
pv++;
a += da;
} z += dz;
}
// Заполнить список граней
int iFirst = iRSteps;
for (iZ = 0; iZ « iZSteps; iZ++) {
for (int iR = 0; iR « iRSteps; iR++) {
*pfd++ =4; //No. of vertices per face
*pfd++ = iFirst + iR;
*pfd++ = iFirst + ((iR + 1) % iRSteps);
*pfd++ = iFirst - iRSteps +
((iR + 1) % iRSteps) ;
*pfd++ = iFirst - iRSteps + iR;
} iFirst += iRSteps;
} *pfd =0; // Завершить список
// Создать круговую поверхность с автоматической // генерацией нормалей
BOOL b = Create(Vertices, iVertices, NULL, 0, FaceData, TRUE) ;
delete [] FaceData;
FaceData = new int [iRSteps * 2 + 2] ;
D3DVECTOR nvect [] = { {0, 0, 1}, {О, 0, -1}
};
if (bClosedl) { pfd = FaceData;
*pfd++ = iRSteps;
for (int iR = 0; iR « iRSteps; iR++) (
*pfd++ = iR;
*pfd++ = 1;
}
Тела вращения тЩ^ 109
*pfd = 0;
m_hr = m_pIMeshBld-»AddFaces(iVertices, Vertices, 2, nvect,
ULONG*)FaceData, NULL) ;
ASSERT(SUCCEEDED(m_hr)) ;
}
if (bClosed2) { pfd = FaceData;
*pfd++ = iRSteps;
iFirst = iRSteps * iZSteps;
for (int iR = 0; iR « iRSteps; iR++) (
*pfd++ = iRSteps - 1 - iR + iFirst;
*pfd++ = 0;
}
*pfd = 0;
m hr = m pIMeshBld-»AddFaces (iVertices, Vertices, 2, nvect,
(ULONG*)FaceData, NULL) ;
ASSERT(SUCCEEDED(m_hr)) ;
}
delete [] Vertices;
delete [] FaceData;
m strMame = "Solid of revolution";
return b;
}
На первом этапе, после выполнения инициализации, по функции радиуса заполняется список вершин. Затем генерируются данные боковых граней и создается исходная форма. Если при вызове функции были заданы замкнутые концы фигуры, создается новый набор данных для граней-торцов, однако на этот раз с нормалями, управляющими процессом закраски, чтобы торцы фигуры казались плоскими. Новые грани добавляются к существующей фигуре.
Возможно, вы обратили внимание на то, что фигуре присваивается имя (в данном случае — Solid of Revolution, хранящееся в переменной m_strName). Когда мы будем заниматься выбором объектов в макете, имя сообщит пользователю, какая фигура выбрана им в настоящий момент.
Мы очень кратко пробежались по большому фрагменту программы, и у вас наверняка осталось много вопросов по поводу его работы и назначению отдельных функций. Если вы хотите понять, как устроена функция CreateRSolid, возьмите лист бумаги в клетку, сверните его в трубку и затем представьте себе, что вам потребовалось описать каждое продольное ребро и каждую грань этой решетки. Именно это и происходит в приведенном выше фрагменте, а эксперимент с трубкой описывает мой подход к его написанию. Во фрагменте присутствуют несколько вызовов функции интерфейсов DirecQD, назначение которых можно узнать в документации по DirectX 2 SDK. Заодно найдите в SDK макрос D3DVAL и посмотрите, что он делает.
/b> ЩЦУ Глава 4. Создание фигур
В главе 5 мы научимся преобразовывать фигуры, применяя к ним операции вращения, переноса и масштабирования. После прочтения этой главы можете модифицировать функцию CreateRSolid так, чтобы при ее вызове можно было бы задать координаты конечных точек фигуры — функция станет более полезной.
Построение ландшафтов
Иногда требуется создать поверхность, которая имитирует пересеченный рельеф местности, холмы или что-нибудь другое, подсказанное вашей фантазией. Приложение Shapes демонстрирует два различных алгоритма для построения случайных рельефов. В первом случае используется решетка из точек, высота которых выбирается случайным образом. Во втором алгоритме грань, в центре которой определяется точка со случайной высотой, делится на несколько вспомогательных граней. Деление повторяется до тех пор, пока количество граней не станет достаточно большим, а ландшафт будет выглядеть достаточно интересно.
Построение ландшафта по решетке
Давайте сначала рассмотрим алгоритм с решеткой. На Рисунок 4-21 изображен пример ландшафта, построенного по решетке из точек со случайной высотой (команда Edit ¦ Landscape 1).
Рисунок. 4-21. Случайный ландшафт, построенный с помощью решетки

Функция для построения поверхности, образующей ландшафт, напоминает функцию для создания тел вращения на стр. 108. В данном случае мы передаем функцию, которая генерирует высоту точки по значениям х и z. Ниже приведен фрагмент приложения Shapes:
Построение ландшафтов
double LandscapeFn(double x, double z, void* pArg)
{
return -2.0 + (double)(rand() % 100) / 100;
// Создать поверхность, изображающую ландшафт void CMainFrame::OnEditInsland()
{
// Создать поверхность с использованием функции высоты
NewScene() ;
m_pShape = new C3dShape;
m_p3hape-»CreateSurface (-5, 5, Т., -10, 10, 1, LandscapeFn, NULL) ;
m_pScene-»AddChild(m_pShape) ;
}
Высота опорных точек определяется случайным образом, а ландшафт создается функцией C3dShape: :CreateSurtace. Данная функция похожа на C3dShape::CreateRSolid, так что я не стану понапрасну утомлять вас подробностями.
Ландшафт, который вы видите на своем экране, может отличаться от изображенного на Рисунок 4-21. Иногда в изображении вдруг появляются странные пики; это явление обусловлено ошибкой в текущей версии DirectX. Более подробная информация, включающая возможные пути борьбы с пиками, приводится в файле Readme.txt на прилагаемом диске CD-ROM. А пока можно попробовать изменить размер окна, чтобы пик исчез из него.
Построение ландшафта делением граней
От смехотворно простого алгоритма перейдем к более серьезному и посмотрим, как строится поверхность в алгоритме деления граней. На Рисунок 4-22 изображен ландшафт, построенный по новому алгоритму (команда Edit ¦ Landscape 2).
Все грани на Рисунок 4-22 выглядят плоскими и имеют острые края, потому что создавшая их функция пользуется отдельным набором вершин для каждой новой грани. Как мы убедились раньше, в разделе «Создание простых фигур» на стр. 97, для той грани, у которой отсутствуют прилегающие грани, по умолчанию создаются нормали вершин, направления которых совпадают с нормалью к грани. Получившаяся грань выглядит плоской. При желании можно модифицировать программу так, чтобы она генерировала нормали вместе с вершинами, или же немного усложнить код и создавать грани с общими вершинами. Давайте сначала рассмотрим алгоритм, по которому создавалась поверхность на Рисунок 4-22, а затем — исходный текст программы.
Внутри каждой грани поверхности выбирается точка. Я решил определять положение этой точки, усредняя координаты всех вершин грани. Выбрав точку,
/b> ^^?1 Глава 4. Создание фигур
Рисунок. 4-22. Ландшафт, построенный по алгоритму деления гранен

которой суждено превратиться в отдельную вершину, мы генерируем случайную высоту для новой вершины и создаем новый набор граней. На Рисунок 4-23 показана прямоугольная грань, разделенная в соответствии с алгоритмом.
. Грань, разделенная на четыре новые грани

После того как будут созданы четыре новые грани, процесс повторяется — четыре новые треугольные грани делятся на новые треугольники, как показано на Рисунок 4-24.
На рисунке довольно трудно понять пространственное положение всех граней, однако вы наверняка уловили общий принцип. Если немного поработать над алгоритмом, он позволит строить довольно реалистичные горы. Давайте посмотрим, как выглядит функция для построения ландшафтов, подобных изображенному на Рисунок 4-22:
Построение ландшафтов
/h2>
Рисунок. 4-22. Грани после повторного деления

void CMainFrame::OnEditInsland2() (
// Создать исходную фигуру, которая является
// простейшей прямоугольной гранью. double х = 10;
double zl = -10;
double z2 = 20;
D3DVECTOR vlist [] = {
(-x, -4, zl},
{-x, -4, z2},
( x, -4, z2},
{ x, -4, zl) };
int nv = sizeof(vlist) / sizeof(D3DVECTOR);
int flist [] = {4, 0, 1, 2, 3,
0 };
NewScene();
m_pShape •= new CSdShape;
m_p3hape-»Create (vlist, nv, flist);
// Делить грани на более мелкие int iCycles = 5;
double dHeight = 1.0;
while (iCycles-) (
// Получить текущий список граней int nPaces = m_pShape-»GetFaceCount () ;
IDirectSDRMMeshBuilder* pMB = m_p3hape-»GetMeshBuilder () ;
ASSERT(pMB) ;
IDirect3DRMFaceArray* pIFA = NULL;
HRESULT hr;
hr = pMB-»GetFaces (SpIFA) ;
ASSERT(SUCCEEDED(hr)) ;
/h2>
Глава 4. Создание (ЬИГУО
// Создать новую фигуру, к которой // будут добавляться новые грани C3dShape* pNewShape = new C3dShape;
// Перебрать грани из списка
for (int iFace = 0; iFace « nFaces; iFace++) {
IDirect3DRMFace* pIFace = NULL;
hr = pIFA-»GetElement (iFace, • SpIFace) ;
ASSERT(SUCCEEDED(hr)) ;
ASSERT(pIFace) ;
// Получить количество вершин DWORD nVert = pIFace-»GetVertexCount () ;
// Разместить буферы D3DVECTOR* pVert = new D3DVECTOR [nVert];;
// Получить данные вершин
hr = pIFace-»GetVertices (&nVert,
pVert, NULL) ;
ASSERT(SUCCEEDED(hr));
ASSERT(pVert) ;
ASSERT(nVert » 2) ;
// Выделить память для новых списков вершин и граней D3DVECTOR* NewVert = new D3DVECTOR [nVert + 1];
int* NewFaceData = new int [4 * nVert + 1] ;
// Скопировать старые вершины //и определить суммы координат C3dVector vNew(0, О, О);
for (DWORD i = 0; i « nVert; i++) (
NewVert [i] =pVert[i];
vNew.x += pVert[i].x;
vNew.y += pVert[i].y;
vNew.z += pVert[i].z;
}
// Вычислить положение новой вершины // на плоскости грани vNew.x /= nVert;
vNew.y /= nVert;
vNew.z /= nVert;
// Прибавить случайное отклонение высоты double dh " dHeight * (1.0 - ((double)(rand() * 100)) / 50.0);
Построение ландшафтов '•'^Щ 115
vNew.y += dh;
// Добавить новую вершину NewVert[nVert] = vNew;
// Создать данные граней int *pfd = NewFaceData;
for (i = 0; i « nVert; i++) (
*pfd++ = 3;
*pfd++ = i;
*pfd++ = (i+1) % nVert;
*pfd++ = nVert; // Новая вершина
} *pfd = 0;
// Включить новые грани в фигуру pNew3hape-»AddFaces (NewVert, nVert+1, NULL, 0, NewFaceData) ;
// Удалить списки вершин и граней delete [] NewVert;
delete [] NewFaceData;
// Удалить данные вершин delete [] pVert;
// Освободить грань pIFace-»Release () ;
}
// Освободить массив граней pIFA-»Release () ;
pMB-»GenerateNormals () ;
// Примечание: не освобождайте интерфейс // построения сеток!!!
// Удалить старую фигуру и сделать текущей новую. delete m_pShape;
m_pShape = pNewShape;
}
// Присоединить итоговую фигуру к макету m pScene-»AddChild(m pShape) ;
Как я уже говорил, такой подход оказывается несколько более трудоемким, чем простая генерация решетки со случайными значениями высоты. Я не стану
/b> 1W Глава 4. Создание фигур
подробно объяснять весь приведенный фрагмент, а предлагаю читателю разобраться с ним самостоятельно. Здесь присутствуют несколько функций класса C3dShape и прямые обращения к интерфейсам механизма визуализации в тех случаях, когда соответствующий сервис не вошел в класс C3dShape.
Создание леса
Давайте попробуем изобразить на экране сценку из жизни леса: в ветвях весело щебечут птички, журчит ручеек, где-то ухает филин. Неплохая мысль — но для начала придется нарисовать что-нибудь, хотя бы отдаленно напоминающее дерево. На Рисунок 4-25 изображена елка (команда Edit ¦АТгее).
Рисунок. 4-25. Елка

Конечно, елки бывают и покрасивее, но пока сойдет и такая. Наше дерево состоит из 25 вершин и 19 граней. Если мы хотим создать целый лес из 100 деревьев (из остальных елок сделали бумагу для книги, которую вы читаете), можно включить в макет еще 99 деревьев, похожих на Рисунок 4-25. Самое время подумать о том, как приказать механизму визуализации нарисовать еще 99 деревьев, в точности аналогичных первому, но расположенных в других местах макета.
Помните, что мы говорили о фреймах и визуальных элементах в главе З? Объект C3dShape содержит фрейм, определяющий его положение, размер, ориентацию и т. д., а также визуальный элемент, который по сути дела описывает набор вершин, граней и т. д. для объекта, который мы хотим увидеть на экране. Функция C3dShape::Clone позволяет включить один и тот же визуальный элемент в несколько разных фреймов. Она создает новый объект C3dShape по существующему объекту, но вместо того, чтобы строить для него новый визуальный элемент, она присоединяет к объекту визуальный элемент исходной фигуры. Таким образом, чтобы изобразить лес, можно создать одно дерево и продублировать его 99 раз. Результат изображен на Рисунок 4-26 (команда Edit ¦ A Forest).
Создание леса
/h2>
Рисунок. 4-26. Лес

Давайте рассмотрим функцию, в которой строится лес, поскольку некоторые аспекты процесса дублирования оказываются неочевидными.
void CMainFrame::OnEditForest() {
NewScene();
// Создать первое дерево вместе со стволом m_pShape = new C3dShape;
m_pShape-»CreateCone (0, О, О, 1, TRUE, 0, 4, О, О, FALSE) ;
C3dShape trunk;
trunk.CreateRod(0, -2, О, О, О, О, 0.2);
m_pShape-»AddChild(&trunk) ;
// Присоединить дерево к макету m_pScene-»AddChild(m_pShape) ;
// Получить позицию и ориентацию ствола // по отношению к родителю (дереву) C3dVector p, d, u;
trunk.GetPosition(p) ;
trunk.GetDirection(d, и);
// Дублировать дерево 99 раз for (int i = 0; i « 99; i++) {
// Дублировать крону и ствол
/h2>
Глава 4. Создание фигур
C3dShape* pTree == m_pShape-»Clone () ;
C3dShape* pTrunk = trunk.Clone();
pTree-»AddChild(pTrunk) ;
// Задать относительную позицию ствола //по отношению к кроне pTrunk-»SetPosition (p) ;
pTrunk-»SetDirection(d, u) ;
// Присоединить дубли как потомков первого дерева, // чтобы можно было вращать весь лес m_pShape-»AddChild(pTree) ;
// Задать положение нового дерева в макете
pTree-»SetPosition( ( (double) (rand () % 100) / 5)
- 10.0,
0,
(double)(rand() % 100) / 5,
ni_pScene);
// Удалить контейнеры delete pTrunk;
delete pTree;
} )
Непременно обратите внимание на то, что ствол присоединяется в качестве потомка к конусу, образующему крону дерева, поэтому при дублировании кроны со стволом важно, чтобы при присоединении ствола-дубликата к кроне-дубликату была сохранена их относительная позиция. Если этого не сделать, ствол будет развернут в каком-нибудь странном направлении и по всей вероятности вообще не будет соединен с кроной. Попробуйте закомментировать фрагменты позиционирования (pTree-»SetPosition) и ориентации ствола и заново постройте приложение, чтобы посмотреть, что из этого получится.
Второй важный момент заключается в том, что деревья-дубликаты становятся потомками самого первого дерева, чтобы можно было вращать весь лес с помощью одной переменной m_pShape (первое дерево). Поскольку дубликаты являются потомками первого дерева, их позиция должна быть задана по отношению ко всему макету. Если удалить из вызова pTree-»SetPosition необязательный аргумент-фрейм (m_pShape), позиция будет указываться по отношению к родителю, и деревья расположатся неверно. Проверьте!
Довольно о фигурах
О фигурах сказано вполне достаточно. Мы научились создавать простейшие грани и более сложные твердые тела. Кроме того, мы увидели, как направление нормалей влияет на закраску и как фигур»! дублируются при повторном использовании их визуальных компонентов. В следующей главе мы научимся перемещать фигуры и изменять их размер и ориентацию посредством преобразований.
Спрайты
Глава 9 Спрайты
Рисунок. 9-1. Картонные фигурки в макете

Ради правдоподобия фигурки на Рисунок 9-1 стоят на подставках. Любой ребенок скажет вам, что без подставок фигурка немедленно упадет. У наших спрайтов нет никаких подставок, но они будут стоять вполне нормально.
Давайте прикинем, как будет выглядеть макет с картонными фигурками на Рисунок 9-1 для зрителя. Если наблюдатель постоянно находится перед макетом, то персонажи будут смотреться вполне нормально, причем дальние фигурки будут казаться меньше ближних. Возможный вид макета изображен на Рисунок 9-2.
/h2>
Рисунок. 9-2. Вид спереди для макета, изображенного на Рисунок 9-1

Теперь подумайте, что произойдет, если наблюдатель посмотрит на макет сбоку. Картонные фигурки не имеют толщины, и поэтому для наблюдателя они исчезнут. А если бы каждая фигурка могла вращаться, чтобы она всегда оказывалась обращена к наблюдателю лицевой стороной? Наблюдатель двигался бы куда угодно и при этом все равно видел фигурку.
Однако в таком случае изображение всегда будет оставаться одним и тем же, что не очень правдоподобно. Обычно сзади люди выглядят несколько иначе, чем спереди. Допустим, человек собирается напасть на вас. Он не будет спокойно следить за тем, как вы подходите к нему со спины, и развернется к вам лицом.
Разворачивая фигурки к наблюдателю, мы сможем имитировать таких картонных агрессоров. К сожалению, среднестатистический бандит выглядит не так статично, как картонная фигурка. Следовательно, нам придется не только следить за ориентацией фигурки, но и изменять ее внешний вид, чтобы она казалась подвижной.
Если мы создадим несколько вариантов изображения для персонажа, поместим один из них в макет так, чтобы он был постоянно обращен лицевой стороной к наблюдателю, и при необходимости будем изменять вид изображения, то у нас появится вполне приемлемая альтернатива построению сложных трехмерных фигур из отдельных граней.
Реализация спрайтов
Спрайты, подобно текстурам, можно размещать в любом месте и масштабировать до любых размеров. Текстуры накладываются на грани любой формы; если бы можно было создать текстуру неправильной формы, у нас почти получился бы
/b>
Глава 9. Спрайты
спрайт. Однако на практике оказывается, что форма текстуры вовсе не обязательно должна быть неправильной. Сама текстура может быть и прямоугольной, если при этом сделать некоторые ее участки прозрачными. Задавая прозрачный цвет для текстуры, фактически мы создаем изображения произвольной формы.
До настоящего момента мы не рассматривали прозрачных изображений, потому что большинство трехмерных объектов представляют собой твердые тела, и при их раскрашивании от прозрачности не будет никакого прока. Прозрачность реализуется достаточно просто — один из цветов назначается «прозрачным», и во время воспроизведения все пиксели данного- цвета просто не копируются из источника (обычно текстурного покрытия) в приемник (буфер воспроизведения).
Текстуры не обладают лишь одним атрибутом, необходимым для создания спрайтов — определенным положением в макете. Эту проблему можно решить, присоединяя текстуру к фрейму. Фрейм предоставляет информацию о положении, а текстура — визуальный компонент.
Механизм визуализации особым образом работает с текстурами, присоединенными к фреймам. Они всегда воспроизводятся в плоскости ракурса — и потому они гарантированно обращены лицевой стороной к наблюдателю. Кроме того, текстуру можно масштабировать в зависимости от ее удаленности по оси г. Положение текстуры выбирается таким образом, чтобы базовая точка текстуры (выбираемая произвольно) находилась в определенной точке фрейма. По умолчанию базовая точка растрового изображения расположена в левом верхнем углу, поэтому при позиционировании текстуры левый верхний угол должен находиться в точке фрейма с координатами х, у, z. Как мы увидим позднее, базовую точку можно переместить — например, в середину нижнего края изображения, и такое ее положение будет более логичным при размещении персонажей в макете. На Рисунок 9-3 изображены: стандартное положение базовой точки (слева) и более логичный вариант (справа).
Рисунок. 9-3. Различные положения базовой точки при размещении спрайта
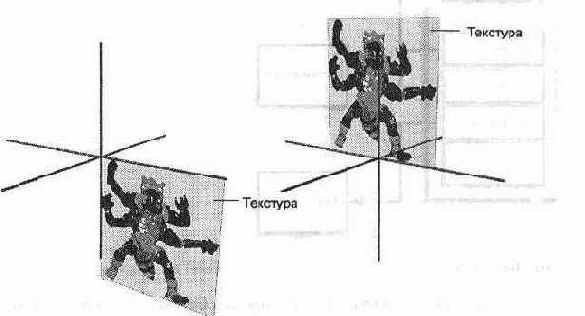
Реализация спрайтов
/h2>
По умолчанию прозрачным цветом считается черный. На мой взгляд это неудобно, поскольку нарисовать растровое изображение на черном фоне довольно сложно. Интерфейс текстур содержит функцию SetDecalTransparentColor, которая назначает другой прозрачный цвет. На момент написания книги мне так и не удалось заставить эту функцию работать, так что пришлось в своих картинках использовать черный цвет в качестве прозрачного. Впрочем, нам нужен хотя бы один работающий прозрачный цвет, и он у нас имеется.
Работа с несколькими изображениями
Некоторые спрайты состоят всего из одного изображения. Например, для кубка одного изображения будет вполне достаточно — форма спрайта остается постоянной, так как кубок с любой стороны выглядит одинаково. Тем не менее для большинства спрайтов все же требуется несколько изображений, и мы должны научиться создавать по ним объект-спрайт. Я называю такие изображения-компоненты фазами, поскольку с изменением фазы изображение движется — это похоже на чередование фаз Луны.
Тривиальное решение
Самый очевидный способ создания спрайта с несколькими изображениями заключается в том, чтобы создать для каждой фазы отдельное изображение в отдельном растровом файле и загружать их в массив текстур, как показано на Рисунок 9-4.
Рисунок. 9-4. Использование нескольких отдельных изображений для создания спрайта

Такая методика достаточно проста и надежна. Спрайт-объект следит за тем, какое изображение в данный момент времени присоединено к фрейму в качестве визуального элемента. Когда потребуется сменить изображение в макете, мы уда-
/h2>
Глава 9. Спрайты
ляем из фрейма текущий визуальный элемент и присоединяем вместо него новый. Поскольку все эти операции производятся с указателями, они работают очень быстро. Сначала моя версия класса C3dSprite была основана именно на этом принципе, поскольку я не мог прочесть полную документацию по механизму визуализации и создать что-нибудь получше — поэтому я точно знаю, что данный метод работает.
Тем не менее есть два важных довода против использования отдельных изображений. Во-первых, на хранение структур данных с большими изображениями и текстурами расходуется много памяти. Во-вторых,' поддержка общей палитры для всех изображений достаточно затруднительна, поскольку файлы никак не связаны друг с другом и могут редактироваться по отдельности.
Лучшее решение
Я предпочитаю создавать спрайты по одному растровому изображению, в котором хранятся все возможные состояния спрайта. Работа с одним растром во многих случаях оказывается более удобной, поскольку при этом очень мало избыточных данных. Например, на Рисунок 9-5 показано растровое изображение с различными фазами спрайта бегущей собаки, использованного в одном из приложений книги «Animation Techniques in Win32» (Microsoft Press, 1995).
Рисунок. 9-5. Полоска из нескольких изображений, используемых при создании спрайта с несколькими фазами, объединенных в одном растре

Работа с несколькими изображениями '''lit 221
Все кадры в такой полоске имеют одинаковый размер, и в них используется одинаковая палитра. При этом вам будет труднее пропустить кадр или перепутать их порядок и легче выдержать постоянство цветов в различных фазах спрайта.
Полоска может иметь и другие размеры — скажем, семь собак в ширину и одну собаку в высоту, или же может состоять из рядов по четыре собаки — как вы считаете нужным. Раз вы знаете точное положение каждого кадра в таком изображении, то сможете написать код для извлечения любого из них. Вертикальное расположение кадров немного упрощает программу. Поскольку для вас, вероятно, не имеет особого значения, как именно расположены кадры спрайта, я бы предложил выбрать тот вариант, который облегчает вашу работу.
Создание текстуры по полоске изображений
Следующий вопрос: как же создать текстуру по полоске изображений?
Для того чтобы создать текстуру, необходимо присоединить изображение к структуре данных, которая описывает работу с изображением при воспроизведении текстуры. Изображение состоит из заголовка и собственно графических данных. Связь между ними изображена на Рисунок 9-6.
Рисунок. 9-6. Строение текстуры

Сначала я решил, что самый естественный способ сменить фазу спрайта — просто обновить значение указателя в заголовке, чтобы он ссылался на другой набор графических данных. К сожалению, на момент написания книги механизм визуализации требовал, чтобы адрес графических данных оставался неизменным. Следовательно, вместо того чтобы изменять указатель, нам придется обновлять данные. На практике это означает, что в вашей полоске изображений должен присутствовать один пустой кадр, используемый в качестве рабочей области. В этом кадре будет создаваться исходная текстура. Если нам понадобится изменить вид спрайта, мы просто копируем нужные графические данные в рабочую область и сообщаем механизму визуализации об изменении текстуры. На Рисунок 9-7 показано, как это происходит.
В момент создания текстуры, высота всего изображения, хранящаяся в соответствующем поле заголовка растрового изображения, заменяется высотой одного кадра. Наверное, вы уже поняли, почему так удобно иметь дело с вертикальной полоской: изображение элементарно делится на кадры, если их высота остается
/b> ЩУ Глава 9. Спрайты
Создание текстуры на основе растра с несколькими кадрами
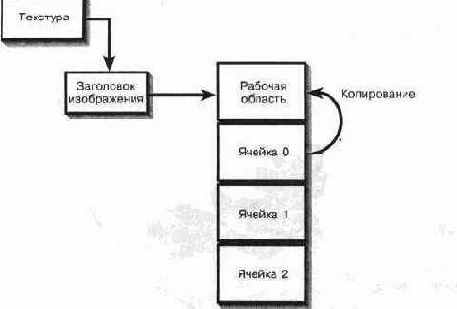
неизменной, а копирование любого кадра в рабочую область осуществляется функцией memcpy или аналогичной ей.
ПРИМЕЧАНИЕ
Возможно, в более поздних версиях Direct3D будут разрешены непосредственные манипуляции с графическими данными, что позволит обойтись без копирования.
Создание растровых изображений
Создание растровых изображений, из которых состоит спрайт, требует некоторого предварительного планирования. Если ваше приложение должно работать в системе с 256 цветами, следует в первую очередь подумать о том, как в растре будут использоваться цвета. Если в ней поддерживается больше цветов, вы обладаете большей свободой в создании изображений.
Поскольку я абсолютно лишен каких-либо художественных способностей, пришлось создавать растровые изображения с помощью видеокамеры и карты захвата видео. Я снимал пластиковую игрушку одного из своих детей. Специалисты по компьютерной графике умеют творить чудеса с помощью своих излюбленных инструментов, но мне пришлось добиваться нужного результата с помощью самых простых средств. На тот случай, если у вас под рукой не окажется художника, я опишу, как я это сделал.
Для создания изображений я воспользовался белой картонной ширмой и фотографическим прожектором. Поставив игрушку на ширму, я установил камеру так, как показано на Рисунок 9-8.
Создание растровых изображений 'i^ 223
Рисунок. 9-8. Домашняя киностудия
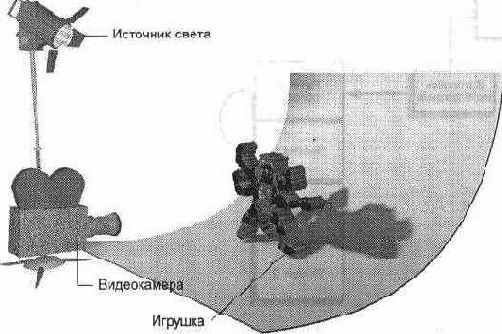
Я придал игрушке агрессивную позу, заснял ее и перенес изображение с видеокамеры на компьютер. Затем я передвинул игрушку в новое положение и сделал новый снимок. Это повторялось до тех пор, пока у меня не появился полный набор кадров с игрушкой, размахивающей руками с явно недружелюбными намерениями. Изображения были сняты в виде 24-битных растров в разрешении примерно 300х200 пикселей.
Я обрезал и масштабировал все изображения до размеров 256'<256 пикселей, а затем перевел их в 8-битный формат (256 цветов) с произвольной палитрой. После того как все изображения были преобразованы, я скопировал одно из них в качестве заполнителя для рабочей области в финальном растре. Затем я присвоил рабочей области имя SOO, а кадры назвал S01, S02 и т. д.
Далее я воспользовался программой, написанной мной для книги по анимации, для того, чтобы взять серию изображений, преобразовать их к единой палитре и построить полоску со всеми изображениями. Программа называется Viewdib и находится в каталоге Tools. В результате получился растровый файл, напоминающий Рисунок 9-5, за исключением того, что верхний кадр в нем представляет собой копию одного из других кадров.
Затем я удалил все посторонние детали (тени, отражения и т. д.), чтобы оставить чистое изображение игрушки, и заполнил окружающий фон черным (прозрачным) цветом. Разумеется, это значит, что в вашем изображении не может использоваться черный цвет. Если вы хотите использовать черный в качестве прозрачного цвета и при этом ваше изображение должно содержать черные участки, замените черный цвет в изображении другим оттенком (например, вместо RGB: 0, 0, 0 можно использовать RGB: О, О, 1). Наконец, я воспользовался Microsoft Imager, чтобы сократить количество цветов с 256 до 8. Результат изображен на Рисунок 9-9.
/b> ЦЩ^ Глава 9. Спрайты
Изображения для составного спрайта

ПРИМЕЧАНИЕ
Верхний кадр является точной копией кадра, расположенного под ним, и резервирует место под рабочую область в графических данных текстуры.
Должен сказать, что это занятие оказалось на редкость нудным. Мой низкий поклон тем, кто подобным образом зарабатывает себе на хлеб. Нам остается лишь написать программу.
Класс C3dSprite
Давайте посмотрим, как устроен класс для работы с фреймом и изображениями, из которых состоит спрайт, и как им пользоваться в приложении. Одна часть
/b>
Создание растровых изображений
кода находится в классе C3dlmage, а другая — в классе C3dSprite. Класс C3dlmage содержит функции для загрузки растрового изображения и деления его на кадры. Для работы с текстурами, необходимыми для создания анимационного спрайта, класс C3dSprite пользуется услугами класса C3dTexture, производного от C3dlmage. На самом деле здесь нет ничего сложного, поэтому давайте рассмотрим процесс создания спрайта и на ходу заполним возможные пробелы. Класс C3dSprite определяется в 3dPlus.h следующим образом:
class C3dSprite : public C3dFrame
{
public:
DECLARE_DYNAMIC(C3dSprite) ;
C3dSprite() ;
virtual --C3dSprite () ;
BOOL Create(C3dScene* pScene,
double x, double y, double z, double scale, UINT uiIDBitmap, int iPhases = 1);
BOOL SetPhase(int iPhase) ;
int GetNumPhases() {return m_Tex.GetNumPhases (); } int GetPhasef) {return m_Tex.Get Phase();}
protected:
C3dTexture m_Tex;
};
Обратите внимание — класс C3dSprite является производным от C3dFrame, и его членом является объект C3dTexture. Мы подробно рассмотрим две функции, Create и SetPhase, поскольку именно они выполняют основную работу объекта-спрайта. Функция Create спроектирована так, чтобы включение спрайта в макет происходило как можно проще. Давайте подробно рассмотрим ее, шаг за шагом.
BOOL C3dSprite::Create(C3dScene* pScene,
double x, double у, double z, double scale, UINT uiIDBitmap, int iPhases) (
ASSERT(pScene) ;
ASSERT(iPhases » 0);
ASSERT(uiIDBitmap) ;
// Создать фрейм и включить его в список фигур макета C3dFrame::Create(pScene) ;
pScene-»m_ShapeList .Append (this) ;
// Установить фрейм в заданное положение SetPosition(x, у, z);
/b> Д¦^ Глава 9. Спрайты
// Загрузить растровое изображение для создания текстуры if ( !m_Tex.C3dIniage: :Load (uiIDBitmap) ) {
TRACE("Failed to load texture image\n");
return FALSE;
}
// Задать количество фаз m_Tex.C3d!mage::SetNumPhases(iPhases) ;
// Создать текстуру по растровому изображению m_Tex.Create ();
// Задать свойства IDirect3DRMTexture* pITex = m_Tex.Getlnterface ();
ASSERT(pITex) ;
// Разрешить глубинное масштабирование m_hr = pITex-»SetDecalScale (TRUE) ;
ASSERT(SUCCEEDED(m_hr)) ;
// Задать исходный размер double a = (double)m_Tex.GetWidth() / (double)m_Tex.GetHeight();
m__hr = pITex-»SetDecalSize (scale * a, scale);
ASSERT(SUCCEEDED(m_hr)) ;
// Разрешить прозрачность m hr = pITex-»SetDecalTransparency(TRUE);
ASSERT(SUCCEEDED(m_hr)) ;
// Назначить прозрачным цветом черный m hr = pITex-»SetDecalTransparentColor(RGB_MAKE(0, 0, 0)) ;
ASSERT(SUCCEEDED(m_hr)) ;
// Перенести начало координат фрейма // в середину нижней стороны m_hr = pITex-»SetDecalOrigin (m_Tex. GetWidth () /2, m_Tex.GetHeight 0-1) ;
ASSERT(SUCCEEDED(m_hr)) ;
// Присоединить текстуру в качестве визуального элемента return AddVisual(&m_Tex) ;
}
Прежде всего необходимо создать объект C3dFrame (базового класса C3dSprite). Мы включаем спрайт в макет и задаем начальное положение фрейма в макете. Далее загружается растровое изображение для текстуры из ресурса BITMAP, добавленного с помощью AppStudio. Обратите внимание на то, что мы вызываем
Создание оастоовых изобоажении ^Sil 227
функцию C3dlmage::Load базового класса, а не функцию класса C3dTexture. Это сделано для того, чтобы иметь возможность слегка изменить изображение перед тем, как создавать по нему текстуру.
После того как изображение загружено, для него задается количество кадров (iPhases). Кадр, используемый в качестве рабочей области, не считается. После того как изображение будет разделено на кадры, мы создаем текстуру. Возможно, код получился некрасивым, но зато он достаточно эффективен и позволяет создавать многофазные спрайты, практически не обращаясь к коду классов текстуры и растрового изображения.
После того как мы получаем указатель на интерфейс IDirect3DRMTexture вызовом функции Getlnterface, необходимо разрешить глубинное масштабирование, чтобы размер спрайта изменялся в зависимости от его положения по оси z. Исходный размер изображения задается в соответствии с масштабным коэффициентом, передаваемым в виде аргумента функции Create. Масштабный коэффициент позволяет задавать размер спрайта независимо от размера растрового изображения. Небольшой дополнительный фрагмент кода обеспечивает сохранение пропорций изображения-оригинала. Поскольку текстуры (и, следовательно, ваши спрайты) разрешается масштабировать в обоих направлениях, при желании вы можете сделать своих персонажей низенькими и толстыми или, наоборот, — высокими и тощими. Думаю, что графические изображения большей частью создаются такими, какими они должны выглядеть на экране, поэтому важно сохранять правильные пропорции.
Далее мы разрешаем использование прозрачности в текстуре. Прозрачным цветом назначается принятый по умолчанию черный. Я сделал это, чтобы продемонстрировать вам, как вызывается функция SetDecalTransparentColor. В прошлом я пользовался и другим подходом — назначал прозрачным цвет левого верхнего пикселя изображения. Это дает значительно больше свободы при разработке графики, поскольку изображение можно окружить любым цветом при условии, что данный цвет не используется в самом изображении.
Последним шагом в создании текстуры является перенос начала координат фрейма в середину нижнего края изображения. Мне показалось, что с этой точкой будет удобно работать, особенно тогда, когда спрайт должен стоять «на поверхности земли» — в данном случае для правильного расположения спрайта достаточно присвоить его координате у значение координаты у поверхности.
После того как текстура создана, остается лишь включить ее в качестве визуального элемента фрейма. Теперь наш спрайт будет виден на экране при воспроизведении макета.
Изменение фазы
Чтобы изменить фазу спрайта, следует вызвать функцию C3dSprite::SetPhase и передать ей номер новой фазы:
BOOL C3dSprite::SetPhase(int iPhase) f
return m_Tex.SetPhase(iPhase);
Работа этой функции сводится к вызову C3dlmage::SetPhase:
/b> Я? Глава 9. Спрайты
BOOL C3dlmage::SetPhase(int iPhase)
{
if ((iPhase « 0) ¦I (iPhase »= m_iPhases)) f return FALSE;
} m iCurPhase = iPhase;
// Скопировать графические данные нужной фазы в рабочую
область
int iBytes = m_rlimg.bytes_per_line * m_rlimg.height;
memcpy(m rlimg.bufferi,
(BYTE*)m_rlimg.bufferl + (m_iCurPhase + 1) *
iBytes,
iBytes) ;
// Известить производные классы об изменениях _OnImageChanged() ;
return TRUE;
}
Приведенный выше фрагмент реализует операцию копирования, изображенную на Рисунок 9-7. Мы вычисляем адрес нужного кадра, затем функцией memcpy копируем данные кадра в рабочую область. После завершения копирования вызывается функция _OnlmageChanged. Эта виртуальная функция класса C3dlmage не делает ничего, однако она может быть переопределена в производных классах (таких, как C3dTexture), которым необходимо сообщать о внесении изменении в изображение. Класс C3dTexture с помощью этой функции, расположенной в файле 3dlmage.cpp, уведомляет механизм визуализации об изменении графических данных текстуры:
// виртуальная функция
void C3dTexture::_OnImageChanged()
{
if (!m pITexture) return; // Возможно, текстура еще не
создана
// Новое изображение — известить механизм визуализации // об изменении графических данных (но не палитры!) m hr = m pITexture-»Changed(TRUE, FALSE);
ASSERT(SUCCEEDED(m_hr)) ;
}
При этом крайне важно уведомить механизм визуализации об изменении графических данных, поскольку они могут кэшироваться; простое обновление графических данных еще не гарантирует изменения макета на экране.
Создание растровых изображений ''IfHj 229
Приложение Sprites
Когда я пишу приложение-пример, то стараюсь избегать всего, что не является абсолютно необходимым для раскрытия темы. Стоило мне наладить работу класса C3dSprite в приложении Sprites, как тут же немедленно захотелось добавить в него массу новых возможностей. Тем не менее я устоял перед искушением, и результат моих усилий можно в первом приближении назвать игрой.
Приложение Sprites — это DOOM- образная игра. Если вам еще не приходилось иметь дело с DOOM, ребята из Id Software наверняка с большим удовольствием продадут вам ее (но пожалуйста, не заказывайте игру сейчас, иначе вы никогда не закончите читать эту книгу!)
Основная цель игры (моей, а не DOOM!) — выслеживать врагов и издавать громкие звуки, имитирующие выстрелы из оружия, которое бы вам хотелось иметь при себе в подобной ситуации. Действие игры происходит в лабиринте стен, построенных из красного вещества. Стены абсолютно непрозрачны и кажутся довольно прочными, однако вы наделены магическими силами и можете проходить прямо сквозь них. Пол лабиринта покрыт дешевым ковром.
Для этой игры вам понадобится джойстик. Я воспользовался своим SideWinder Pro и настроил его так, чтобы кнопка 1 (гашетка на SideWinder) выполняла стрельбу. Если у вас есть только мышь, вы все равно сможете находить врагов, однако выстрелы придется вообразить. На Рисунок 9-10 показан вид экрана в начале игры — собственно, ничего больше вам знать и не потребуется.
Рисунок. 9-10. Похоже, хозяев нет дома

При разработке этого приложения я воспользовался планом лабиринта, изображенным на Рисунок 9-11 (для самых недогадливых он станет подсказкой).
/b> ¦¦¦И' Глава 9. Спрайты
. План лабиринта

Каждая стена лабиринта состоит из четырех граней, и на каждую грань наложена красная текстура. Для стен я создал класс CWall, производный от C3dShape, код которого мало отличается от того, что мы видели в предыдущих главах, и потому я не стану приводить его. Построение лабиринта с помощью класса CWall происходит следующим образом:
BOOL CMainFrame::NewScene() {
WALLINFO wi [] = {
(-6, 5, 6, 6, 1},
{ 5, -5, 6, 5, 0.9},
{-6, -6, 6, -5, 1.1},
(-6, -5, -5, 5, 0.8},
(-3, 2, 2, 3, 0.5},
( 2, -3, 3, 3, 0.9},
(-4, -1, 0, 0, 1},
(-1, -5, 0, -2, 1.3}
};
int nWalls = sizeof(wi) / sizeof(WALLINFO);
WALLINFO* pwi = wi;
for (int i = 0; i « nWalls; i++) {
CWall* pWall = new CWall(pwi);
m_pScene-»AddChild(pWall) ;
m_pScene-»m_ShapeList .Append (pWall) ;
pwi++;
}
Приложение Sprites
/h2>
Данные для каждой стены состоят из двух наборов угловых координат х и у и высоты. Стены поочередно создаются и включаются в макет.
Пол представляет собой объект с одной гранью, на которую наложена текстура. Для фона макета выбран синий цвет, чтобы создать иллюзию неба над стенами:
m_pScene-»SetBackground(0, О, 1);
CFloor* pFloor = new CFioor(-6, -6, 6, 6) ;
m_pScene-»AddChild (pFloor);
m_pScene-»m_ShapeList .Append (pFloor) ;
Для пола я также завел отдельный класс, но опять же его код ничем не отличается от того, с помощью которого мы создавали объект с одной гранью в главе о цветах.
Последнее, что необходимо добавить в наш лабиринт, — врагов и взрывы. И снова я создал специальные классы для каждого из этих объектов. Они являются производными от C3dSprite, и поскольку оба класса похожи, мы рассмотрим лишь один из них. Ниже приведено определение класса CSoldier (находящееся в файле maze.h), с помощью которого мы создаем себе врагов:
class CSoldier : public C3dSprite
{
public:
CSoldier(C3dScene* pScene, double х, double z) ;
void Update 0;
>;
Как видите, здесь нет ничего сложного: конструктор создает объект, а функция Update заведует его перемещением. Код конструктора (из файла maze.cpp) выглядит следующим образом:
CSoldier::CSoldier(C3dScene* pScene, double х, double z) (
Create(pScene, х, 0, z, 0.5, IDB_SOLDIER, 4);
Должно быть, выше приведена одна из самых простых функций, которые нам приходилось видеть в этой книге. Функция C3dSprite::Create выполняет всю основную работу по созданию объекта-спрайта. Ей передается идентификатор растрового ресурса. Последний аргумент (4) определяет количество кадров в спрайте (не считая рабочей области).
Поскольку спрайты должны двигаться, нам понадобится функция Update для изменения фазы:
void CSoldier::Update() {
SetPhase((GetPhaseO + 1) % GetNumPhases ());
/b> fli"' Глава 9. Спрайты
Данная функция вызывается во время пассивной работы приложения, непосредственно перед обновлением всего макета. Класс для взрывов содержит аналогичную функцию для изменения внешнего вида взрыва со временем.
Постойте, какого еще взрыва?!? А это вы можете выяснить самостоятельно (или в компании врагов).
Довольно о плоских фигурах
Мы выяснили, как пользоваться спрайтами для отображения персонажей или объектов в трехмерной сцене. Как нетрудно убедиться, создавать многогранные фигуры вовсе не обязательно. Спраиты могут использоваться вместе с трехмерными объектами, чтобы обеспечить оптимальное соотношение между качеством изображения и производительностью.
Создание игры отнюдь не сводится к расстановке спрайтов в трехмерном макете. Я даже не пытался показать, как ограничить перемещение игрока в лабиринте или предупредить его о приближающейся опасности. Оставляю эту работу вам — сделайте следующий шаг и реализуйте перечисленные мной функции.
Свет и тень
Глава 10 Свет и тень
Цветовые модели

Перед тем как приступить к полноценной работе с источниками света, мы сделаем небольшой шаг в сторону и посмотрим, каким образом механизм визуализации генерирует цвета. Для того чтобы определить окончательный цвет пикселя в окне, необходимо принять во внимание следующие факторы:
• Цвет и материал поверхности, находящейся непосредственно под пикселем.
• Угол наклона поверхности по отношению к каждому источнику света в макете.
• Цвет, интенсивность и расположение каждого источника света.
• Возможности физического устройства отображения (дисплея).
Упрощая задачу определения цвета пикселя, мы ускоряем выполнение этой операции, и, соответственно, общую скорость работы механизма визуализации.
Существует несколько способов упрощения этой задачи. Например, можно игнорировать цветовые компоненты света и считать их источниками белого цвета различной интенсивности. Это значительно упрощает расчет цветов и ускоряет производительность без особого вреда для качества. Или возьмем другой пример — мы можем упростить зависимость между свойствами материала и его цветом. Для этого зеркальные и диффузные отражающие свойства материала комбинируются, и по ним определяется индекс в цветовой таблице, содержащей весь диапазон цветов объекта, от чисто зеркального до чисто диффузного. Возможно, эти примеры покажутся излишне упрощенными, однако они показывают, что небольшая доля изобретательности может значительно улучшить производительность работы, хотя и за счет качества изображения. Поскольку чаще всего основной проблемой является именно производительность, с небольшой потерей качества вполне можно примириться.
Приведенные выше примеры показывают, что решить проблему цвета можно несколькими способами. Наверное, разработчикам Direct3D следовало позволить нам, пользователям, самим выбирать методику оптимизации для каждого конкретного случая. Тем не менее они этого не сделали. Нам предлагаются всего два режима: монохромный и RGB. Монохромный режим назван так из-за того, что в нем используются только монохромные (белые) источники света. Мы можем менять интенсивность источника света, но не его цвет. Это заметно упрощает процесс обсчета цветовых оттенков. Кроме того, цвета материалов в монохром-Цветовые модели •Щ 235
ном режиме выбираются посредством поиска в таблице. Поиск дает только приблизительный результат. В монохромном режиме применяются многочисленные оптимизации, позволяющие добиться максимальной скорости. Все приложения-примеры, с которыми мы знакомились до настоящего момента, работали именно в монохромном режиме.
В RGB-режиме для расчета цвета пикселей используются значительно более сложные вычисления. RGB-режим полностью поддерживает работу с цветными источниками света и свойствами материала и позволяет получить наилучшее возможное качество изображения. Поскольку в этой главе мы будем играть с цветными источниками света, нам придется настроить механизм визуализации на работу в RGB-режиме. Наверняка вы подумали: «Все, о производительности придется забыть!» Не волнуйтесь, дело обстоит не так плохо.
Наконец, при генерации цветов следует учитывать и физические возможности дисплея, влияющие как на качество, так и на производительность.
• 24-битный дисплей способен отобразить практически любой цвет, сгенерированный механизмом визуализации в виде тройки RGB-компонент. На каждый пиксель необходимо переслать 3 байта данных; в отдельных случаях этот фактор может сказаться на производительности.
• 16-битпь1Й дисплей может отобразить от 32,767 до 65,535 цветов, в зависимости от настройки механизма визуализации. Для каждого пикселя требуется всего 2 байта данных, однако при их генерации приходится выполнить с RGB-компонентами несколько операций сдвига, что также требует некоторых расходов времени.
• 8-битный дисплей (который до сих пор остается наиболее распространенным) отображает всего 256 цветов, причем перед механизмом визуализации встает дополнительная проблема — какой из 256 цветов ему выбрать в каждом конкретном случае? Тем не менее на каждый пиксель в этом режиме приходится пересылать всего 1 байт данных.
Короче говоря, ситуация выглядит следующим образом. При 24-битном дисплее вы получаете потрясающие картинки. При 16-битном дисплее вы получаете хорошее качество с неплохой производительностью, 8-битный дисплей позволяет добиться неплохого качества при хорошей производительности. Основная проблема 8-битных дисплеев заключается в том, что для воспроизведения огромного диапазона цветов RGB-модели при 256-цветной палитре приходится пользоваться методикой смешения цветов (dithering), снижающей общее качество изображения. В монохромном режиме на 8-битном дисплее можно ограничить количество цветов, используемых объектами, и получать все необходимые цвета непосредственно из палитры. При этом вы получаете качественное изображение при хорошей производительности. Чтобы решить, какой режим лучше всего подходит вам, следует немного поэкспериментировать.
Тип цветовой модели задается при создании трехмерного окна. Ниже приведен соответствующий фрагмент кода:
/b> :i^a:i::-' Гпяпя 1П Г!пет u TftHh
int CMainFrame::OnCreate(LPCREATESTRUCT IpCreateStruct)
{
// Создать трехмерное окно
if (!m_wnd3d.Create(this, IDC_3DWND, D3DCOLOR_RGB)) { return -1;
t
Если при вызове функции C3dWnd::Create цветовая модель не указана, по умолчанию принимается значение D3DCOLOR_MONO.
Пожалуй, мы задержались на этой теме несколько дольше, чем я рассчитывал вначале, однако мне хотелось пояснить, почему мы переходим на RGB-модель вместо монохромной, которая до настоящего времени вполне нас устраивала.
Выбор типа освещения
Механизм визуализации DirectSD поддерживает пять разных типов освещения:
рассеянное, направленное, параллельно-точечное, точечное и зональное. Каждый тип освещения обладает определенными свойствами и сложностью обсчета и по-своему влияет на внешний вид макета. В приведенной ниже таблице перечислены свойства каждого из типов освещения.
| Тип освещения | Положение | Направление | Точечный источник | Предельная дальность | Другие параметры |
| Рассеянный | нет | нет | нет | нет | нет |
| Направленный | нет | да | нет | нет | нет |
| Параллельно-точечный | да | нет | да | нет | нет |
| Точечный | да | нет | да | да | нет |
| Зональный | да | да | да | да | да |
Рассеянный свет
Рассеянный свет обсчитывается проще всего. Он обеспечивает равномерный уровень освещения в макете, при котором все грани объектов освещаются одинаково. На Рисунок 10-1 изображен пример макета, освещенного белым рассеянным светом.
/b>
Выбор типа освещения
Рисунок. 10-1. Макет, освещенный только рассеянным светом

ПРИМЕЧАНИЕ
На самом деле свет не имеет определенной формы. Я придал свету форму лишь для того, чтобы вам было удобнее следить за положением источника и перемещать его для изменения освещенности.
Вопреки первому впечатлению, эти джентльмены вовсе не собираются грабить банк. «Эффект чулка» вызван сочетанием плоского освещения и смешением цветов, необходимым для отображения объекта на моем 256-цветном дисплее. От одного рассеянного света проку мало, однако в сочетании с другими типами освещения он помогает устранить из макета излишне темные области.
Направленный свет
Направленный свет по простоте обсчета уступает разве что рассеянному. Он освещает макет параллельными лучами из источника, находящегося на бесконечно большом расстоянии от макета. Его ориентация задается с помощью вектора направления. Задавать положение источника направленного света бесполезно. На Рисунок 10-2 изображен макет, освещенный рассеянным светом малой интенсивности в сочетании с направленным светом.
Как видите, макет выглядит значительно лучше, чем с одним лишь рассеянным светом. Освещение на Рисунок 10-2 очень похоже на встречающееся в естественных условиях. Стрелка показывает, откуда падает направленный свет. На Рисунок 10-3 изображен тот же самый макет, но без рассеянного света.
Рисунок 10-3 выглядит слишком контрастным, на нем имеется много темных мест, которые мешают рассмотреть некоторые части объектов.
/b>
Глава 10. Свет и тень
Рисунок. 10-2. Направленный свет используется для получения бликов

Макет освещен только направленным светом

Параллельно-точечный свет
Если вы хотите включить в свой макет источник света (например, настольную лампу) и наглядно показать его действие, то наиболее естественным решением оказывается параллельно-точечный источник света. Свет исходит из заданной точки, при перемещении которой изменяется внешний вид макета. Тем не менее, лучи света из такого источника падают параллельно, упрощая все вычисления. Установка параллельно-точечного источника света между двумя головами в нашем макете приводит к результату, изображенному на Рисунок 10-4.
/b>
Выбоо типа освешения
Рисунок. 10-4. Параллельно-точечное освещение

Как видно из рисунка, источник света (изображенный в виде маленького кубика) освещает головы таким образом, что свет кажется исходящим из точки, в которой находится кубик. По Рисунок 10-4 довольно сложно определить глубину источника света по отношению к головам, но если посмотреть на текст программы (мы сделаем это позднее, на стр. 242), то можно убедиться, что источник света находится немного позади от них.
Точечный свет
Точечное освещение во многих отношениях напоминает параллельно-точечное, за исключением того, что при вычислениях лучи считаются расходящимися от источника. При этом изображение получается несколько более реалистичным, как можно убедиться из Рисунок 10-5.
Я советую немного поэкспериментировать с приложением Lights, чтобы понять отличия этого типа освещения от предыдущего. Впрочем, повышение качества обходится довольно дорого, и по моему мнению, точечное освещение не имеет особых преимуществ перед параллельно-точечным.
Зональный свет
Обсчет зонального освещения оказывается самым сложным, однако оно заметно повышает качество изображения, как можно видеть из Рисунок 10-6 (кроме того, посмотрите на цветную версию рисунка на вкладке).
На освещенность макета влияет как положение, так и направление зонального источника света. Кроме того, угол светового конуса изменяется по двум параметрам. Считается, что световой конус состоит из центрального конуса с полной интенсивностью и внешнего конуса с уменьшенной интенсивностью. Вы можете задавать величину угла при вершине обоих конусов. Зональный источник света идеально подходит для создания макета тюремного двора с прожекторами или лесного костра.
/b>
Глава 10. Свет и тень
Рисунок. 10-5. Точечное освещение
Зональное освещение

Выделите немного времени на то, чтобы познакомиться с приложением Lights и посмотреть, как каждый тип освещения влияет на внешний вид макета. В приложении имеются окна диалога, которые позволяют вам регулировать уровень рассеянного света и определять большую часть свойств источников. Кроме того, вы сможете выделять и перемещать источники света в макете, как обычные объекты.
/h2>
Выбор типа освещения
Предельная дальность и затухание
Точечные и зональные источники света обладают еще двумя параметрами, влияющими на освещение макета. Предельная дальность определяет расстояние, на котором действует свет. По умолчанию предельная дальность равна 256 единицам модели — этого хватит для освещения всех объектов, которые мы до настоящего момента включали в макеты. Присвоение данному параметру малых значений приводит к довольно интересным эффектам. Кроме того, при этом повышается производительность работы механизма визуализации, поскольку при расчете освещенности объектов, расстояние до которых превышает предельную дальность источника света, можно не учитывать данный источник.
Другой параметр, величину которого также можно регулировать, — затухание. Он влияет на убывание интенсивности света с расстоянием. В квадратное уравнение, определяющее интенсивность света, входят три параметра. В документации по DirectSD они названы постоянной, линейной и квадратичной составляющими. По умолчанию им присваиваются значения 1, 0 и 0 соответственно — интенсивность света от такого источника не убывает с расстоянием. Уравнение, определяющее величину затухания, выглядит следующим образом:
а = с + Id + qd2,
где а — величина затухания; с — постоянная составляющая; 1 — линейная составляющая; d — расстояние от источника света, a q — квадратичная составляющая. Для того чтобы изменить затухание источника света, можно воспользоваться функцией C3dlight::SetAttenuation.
Хватит разговоров — давайте программировать
Хорошо, что вы меня остановили! Я заговорил на свою любимую тему, о физике, а подобных вещей никогда не следует допускать. Вы даже не успеете понять, что случилось, а я уже начну разглагольствовать о дифракционных решетках и волновых пакетах.
Поскольку программная реализация источников света выглядит довольно просто и не сильно отличается для различных типов освещения, я приведу код только для создания параллельно-точечного источника света на Рисунок 10-4.
void CMainFrame::OnEditParlight() {
C3dParPtLight* pLight = new CSdParPtLight;
pLight-»Create (1, 1, 1);
m_pCurLight = pLight;
// Создать фигуру, изображающую источник света C3dShape* psi = new C3dShape;
psl-»CreateCube (0.2) ;
// Присоединить источник света в качестве потомка фигуры, 242 аШУ Глава 10. Свет и тень
// чтобы его можно было выбрать psl-»AddChild(pLight) ;
// Присоединить источник света к макету m_pScene-»AddChild(psl) ;
m pScene-»m_ShapeList. Append (psi) ;
m pScene-»m_ShapeList. Append (pLight) ;
// Поместить источник света на видном месте psl-»SetPosition(0, 1, -2);
psl-»SetName ("Parallel Point Light");
MakeCurrent(psi) ;
}
Большая часть этого фрагмента не имеет никакого отношения к созданию самого источника света, но мы все равно рассмотрим его. В начальных строках функции определяется источник света — в данном случае объект CSdParPtLight. Чтобы показать расположение источника света в макете, я создал фигуру и присоединил к ней источник в качестве потомка, чтобы они перемещались вместе. Классы фигуры и источника света являются производными от CSdFrame. Это позволяет включить их в список фигур макета, чтобы они были удалены во время уничтожения всего макета. Остается лишь задать положение источника света в макете. Для направленного источника света следовало бы задать направление, а для зонального — как направление, так и положение.
Классы C++ для работы с источниками света конкретного типа выглядят очень просто. Они являются производными от класса C3dLight, в котором и создается источник:
BOOL C3dLight::Create(D3DRMLIGHTTYPE type,
double r, double g, double b) {
// Создать фрейм, содержащий источник света if (!C3dFrame::Create(NOLL)) return FALSE;
// Создать объект-источник света ASSERT(m_pILight == NULL);
if (!the3dEngine.CreateLight(type, r, g, b, &m pILight)) {
return FALSE;
} ASSERT(m_pILight);
// Присоединить источник света к фрейму ASSERT (m_J3l Frame) ;
m_hr = m_pIFrame-»AddLight (m_pILight) ;
if (FAILED(m_hr)) return FALSE;
return TRUE;
}
Хватит оазговооов — давайте поогоаммиоовать "lEU 243
Источник света присоединяется к фрейму для того, чтобы мы смогли задать его положение. Источник света, создаваемый механизмом визуализации, не обладает собственным положением или ориентацией, пока он не будет закреплен за каким-нибудь фреймом. Наследование классом C3dLight свойств класса C3dFrame облегчает работу с объектами в макетах.
Цветные источники света
Я довольно долго искал какой-нибудь пример того, как цветное освещение улучшает вид макета, однако после долгих размышлений мне удалось изобрести лишь несколько простейших приложении, не имеющих никакого практического значения. Затем в один прекрасный день я увидел в чьем-то кабинете пару красно-зеленых стереоскопических очков, и это натолкнуло меня на мысль. Предлагаю вашему вниманию программу для просмотра стереоскопических изображении. Приложение находится в каталоге Stereo. Для работы с ним следует надеть стереоскопические очки. На Рисунок 10-7 показано, как будет выглядеть окно приложения, если вы вдруг снимете очки.
Рисунок. 10-7. Нестереоскопическое изображение стереоскопического объекта в зеленых тонах

Читателей, которым приходилось рассматривать стереокартинки на упаковках с кукурузными хлопьями, может удивить отсутствие на Рисунок 10-7 знакомых красно-зеленых перекрывающихся изображений. Дело в том, что моя программа воспроизводит макет в красном освещении, после чего слегка передвигает камеру и перерисовывает его в зеленом свете. Таким образом, экран может принадлежать либо зеленой, либо красной половинке рабочего цикла. Чтобы добиться полноценного стереоэффекта, запустите приложение Stereo и наденьте стереоскопические очки. При этом желательно выключить свет и остаться в темноте.
94Д •^IStW' Гпап-а 1П Г^ват 1л тош!-
Не знаю, можно ли считать это практическим примером работы с цветным освещением, однако писать программу было довольно интересно. Смысл основной части этого приложения — переместить камеру, задать новое освещение и воспроизвести макет на экране. Давайте выделим несколько минут и посмотрим, как все это делается. Однако перед тем, как заниматься программой, взгляните на Рисунок 10-8, который поясняет принцип ее работы.
Рисунок. 10-8. Получение стереоизображения

Сначала макет освещается красным светом, а камера переносится в точку А, в которой воспроизводится изображение для левого глаза. Затем макет освещается зеленым светом, а камера переносится в точку В, где воспроизводится изображение для правого глаза. Если просматривать изображение с красным фильтром на левом глазу и зеленым — на правом, то левый глаз будет видеть изображение из точки А, а правый — из точки В. Ниже приведен фрагмент кода пассивного цикла приложения, в котором все это происходит:
BOOL CMainFrame::Update() {
m_bPhase = !m bPhase;
double d = 1.0; // Расхождение
double cz = 10; // Положение камеры по оси z
C3dVector vo;
if (m_pCur3hape) (
I iRRTHhIP UrrrrHJUUIUIA ГРОТЯ "ЧКЙ:-; 9А^
m_pCurShape-»GetPosition (vo) ;
} else {
vo = C3dVector(0, 0, 0) ;
} C3dVector cv;
if (m_pDirLight && m_p3cene) { if "(itiJaPhase) {
m_pDirLight-»SetColor (1, 0, 0) ;
cv = C3dVector(-d, 0, -cz') ;
} else {
m_pDirLight-»SetColor(0, 1, 0);
cv = C3dVector(d, 0, -cz);
} m_pScene-»SetCameraPosition (cv) ;
C3dVector vl = vo — cv;
m_pScene-»SetCameraDirection (vl) ;
}
// Обновить трехмерное окно if (m_wnd3d.Update(1)) { ЬМоге = TRUE;
}
return ЬМоге;
i
Вектор текущего положения объекта (vo) используется для вычисления вектора направления камеры (vl), чтобы векторы для левого и правого видов сходились в центре объекта.
Подобный подход к реализации стереоскопического изображения обладает тремя недостатками:
• Поскольку левый и правый виды выводятся по отдельности, изображение заметно мерцает.
• Стереоскопическое изображение невозможно захватить (сфотографировать);
хотя макет остается прежним, приложение должно постоянно перерисовывать его.
• Вывод стереоскопического макета занимает вдвое больше времени, чем для обычного макета, поскольку приходится сначала воспроизводить его в красном освещении, а затем — в зеленом.
Все проблемы такого рода можно было бы решить при одновременном воспроизведении левого и правого видов. На практике это означало бы, что левый вид, состоящий исключительно из красных пикселей, выводится в буфер. Правый вид, состоящий исключительно из зеленых пикселей, накладывается на содержимое буфера, а получившееся изображение воспроизводится на экране. К сожалению, данная версия Direct3D не обладает возможностями по наложению изображений, поэтому скомбинировать два вида в одном буфере нам не удастся.
/b> ЙУ Глава 10. Свет и тень
Тени
В самом начале книги я упомянул о том, что механизм визуализации Direct3D не поддерживает работу с тенями. Тем не менее в отдельных случаях тень все же можно имитировать, создавая визуальный объект нужной формы и размещая его в нужном месте макета. На Рисунок 10-9 изображен пример из приложения Lights (выполните команды File ¦ New и Edit ¦ Insert Shape, нажмите кнопку ОК на вкладке Sphere и выполните команду Edit ¦ Shadow).
Рисунок. 10-9. Имитация тени

Для создания тени следует спроектировать объект на плоскость и указать положение источника света в качестве параметра. Чтобы тень появилась в макете, необходимо присоединить ее к некоторому фрейму. Присоединение тени к фрейму затеняющего объекта обеспечивает перемещение тени вместе с объектом. Кроме того, при движении источника света тень также будет перемещаться. Плоскость, на которую отбрасывается тень, задается с помощью точки и вектора нормали. Приведенный ниже фрагмент создает сферу на Рисунок 10-9 и присоединяет к ней тень:
void CMainFrame::OnEditShadow() (
C3dShape* pCast = new C3dShape;
pCast-»CreateSphere(0.3) ;
m_pScene-»AddChild(pCast) ;
m_pScene-»m_ShapeList .Append (pCast) ;
pCast-»SetPosition(0, 1, 0) ;
MakeCurrent(pCast) ;
// Создать тень, слегка приподнятую над плоскостью
Тени
/h2>
CSctVector pt(0, -1.9, 0); // Точка плоскости
C3dVector normal(0, 1, 0); // Нормаль к плоскости
pCast-»Create3hadow(pLight, pt, normal);
i
Функция C3dShape::CreateShadow создает визуальный элемент тени по нескольким аргументам: текущему источнику света, точке плоскости, на которую отбрасывается тень, нормали к этой плоскости:
BOOL CSdShape::CreateShadow(C3dLight* pLight,
D3DVECTOR& vPt,
D3DVECTOR& vN) {
IDirect3DRMVisual* pIVisual = NULL;
m_hr =
the3dEngine.Getlnterface()-»CreateShadow(GetVisual(), pLight-»GetLight () , vPt.x, vPt.y, vPt.z, vN.x, vN.y, vN.z, SpIVisual);
ASSERT(SUCCEEDED(m_hr)) ;
// Присоединить тень к фрейму ASSERT(m_pIFrame) ;
m_hr = m_pIFrame-»AddVisual (pIVisual) ;
return SUCCEEDED(m_hr);
)
Поскольку тень является таким же визуальным объектом, как и любая другая фигура макета, следует соблюдать осторожность при задании плоскости, на которую она должна проектироваться. Убедитесь, что эта плоскость слегка приподнята над поверхностью, на которую должна отбрасываться тень. Если эта плоскость совпадет с гранью объекта, пиксели перемешаются и результат будет непредсказуемым. Тень, слегка приподнятая над поверхностью, выглядит вполне нормально и четко.
Обратите внимание — тень может проектироваться только на одну плоскость. Вы не сможете загнуть ее за угол или перенести на смежную грань куба. Кроме того, проекционная плоскость считается бесконечной. В демонстрации, изображенной на Рисунок 10-9, перемещение источника света или фигуры выводит тень за пределы поверхности, на которую она проектируется. Кроме того, можно протащить фигуру сквозь поверхность вниз, а тень при этом останется наверху.
Разумеется, тени повышают реализм изображения, однако пользоваться ими следует осторожно, чтобы не разрушить иллюзию. На Рисунок 10-10 изображено окно приложения Globe, рассмотренного в главе 13, в котором тень применяется для улучшения общего вида макета (кроме того, посмотрите на цветной вариант этого рисунка на вкладке).
9АЯ -flaSi^' ГПОП-Э 1П Г^аат 1Л TQLJL
Рисунок. 10-10. Приложение Globe с тенью

Итоги
Различные типы освещения могут значительно улучшить внешний вид макета. Поскольку для некоторых источников света требуются более сложные расчеты, необходимо разумно выбирать тип освещения в тех случаях, когда важна высокая скорость работы приложения. Цветные источники света применяются для создания специальных эффектов, но не забывайте о том, что работать с ними можно только в RGB-модели. Наконец, тени также повышают реализм изображения, но они ограничены всего одной плоскостью.
Удаленная отладка в Visual C++
Удаленная отладка в Visual C++

Приведенные ниже инструкции предполагают, что вы установили Microsoft Windows 95 на обоих компьютерах — на рабочем (ведущем) и на тестовом (ведомом). Кроме того, вы должны установить Visual C++ на ведущем компьютере, соединить ПК посредством локальной сети и установить стек протокола TCP/IP. Условные имена ведущий и ведомый следует заменить именами ваших компьютеров.
1. На ведомом компьютере создайте каталог TEST и задайте его совместное использование с именем TEST и полным доступом без пароля.
2. Скопируйте перечисленные ниже файлы из соответствующего каталога ведущего компьютера (Msdev\bin или WindowsVSystem) в \\TARGET\TEST (здесь и в дальнейшем TARGET заменяется именем ведомого компьютера):
Msvcmon.exe, Msvcrt40.dll, TInOt.dll, DmnO.dll. Эти файлы необходимы для проведения сеансов отладки на ведомом компьютере.
3. Скопируйте ЕХЕ-файл отлаживаемой программы и все необходимые DLL-библиотеки в \\TARGET\TEST.
4. Запустите на ведущем компьютере Visual C++ и выполните команду Tools ¦ Remote Connection. В окне диалога Remote Connection выберите строку Network (TCP/IP) и нажмите кнопку Settings.
5. В окне диалога Win 32 Network (TCP/IP) Settings укажите имя ведомого компьютера или его IP-адрес (например, 199.99.99.9) и введите пароль (например, DEBUG). Вы обязаны заполнить поле с паролем. Нажмите кнопку ОК во всех окнах диалога.
6. На ведомом компьютере запустите программу Msvcmon.exe, выберите из списка строку Network (TCP/IP) и нажмите кнопку Settings.
7. В окне диалога Win 32 Network (TCP/IP) Settings введите имя ведомого компьютера и пароль, заданный на шаге 5.
8. Нажмите кнопку Connect, чтобы начать сеанс отладки на ведомом компьютере. До установления связи с ведущим компьютером открывается окно диалога Connecting.
9. На ведущем компьютере выполните команду Build ¦ Settings в среде Visual C++. В окне диалога Project Settings выберите вкладку Debug. В полях
•ж^
VnanouLJaa /wn-ani/o D \/ienal f^^-J. 'ЧГЙЙ 40'У
Remote Executable Path и File Name введите путь к исполняемому файлу, скопированному на ведомый компьютер на шаге 3 (например, \TEST\D3DEval.exe). Нажмите кнопку ОК.
10. Нажмите кнопку Go в Visual C++, чтобы начать сеанс отладки. Вероятно, на экране появится окно диалога Find Local Module, в котором следует указать местонахождение локальных DLL-библиотек. Введите путь к каждой из них или снимите флажок, который предлагает вам продолжить поиски.
На ведомом компьютере должно запуститься ваше приложение. Ведущий компьютер будет использоваться для отладки. После завершения работы выйдите из приложения и нажмите кнопку Disconnect в окне диалога Connecting на ведомом компьютере. Не забудьте выбрать в списке Remote Connection на ведущем компьютере строку Local.
В случае, если вам не приходилось ранее пользоваться отладчиком Visual C++, подробное описание его работы можно найти в документации.
Отладка с использованием Wdeb386
Если вы хотите получить полный контроль над процессом отладки, вам придется воспользоваться отладчиком Wdeb386. Он позволяет отлаживать любые программы для Windows 95 — приложения, DLL-библиотеки, драйверы устройств, VxD и т. д. Отладчик входит в состав Win32 SDK, который включен в Microsoft Developer Network (II уровень).
Ниже приведены краткие инструкции по запуску Wdeb386. Более подробное описание и перечень команд Wdeb386 можно найти в документации по Win32 SDK.
1. Воспользуйтесь терминалом стандарта RS232 или другим компьютером. Настройте терминал на скорость передачи данных 9600 или 19200 бод. Обычно я задаю для своего терминала 8-битные данные, отсутствие контроля четности и 1 стоп-бит.
2. Подключите терминал к одному из СОМ-портов основного компьютера через нуль-модемный кабель (подробное описание кабельного соединения имеется в сопроводительной документации по установке Wdeb386).
3. Запустите на основном компьютере терминальное приложение (например, HyperTerminal) и убедитесь в правильности пересылки текста на терминал. Наберите на терминале какой-нибудь текст и проверьте, верно ли он передан на основной компьютер. Это позволит быть уверенным в правильности аппаратных настроек.
4. На основном компьютере скопируйте все DLL-библиотеки и символьные файлы из каталога Mstools\debug в Windows\System. Вероятно, для этого вам придется загрузиться в режиме командной строки, поскольку иначе не удастся заместить используемые файлы (такие, как Gdi32.dll). Чтобы загрузить компьютер в режиме командной строки, нажмите клавишу F8 при появлении сообщения Starting Windows во время загрузки и выберите из меню команду Command Prompt Only или выполните команду Shut Down из меню Start Windows 95 и выберите Restart The Computer in MS-DOS Mode.
5. Чтобы запустить сеанс отладки, загрузитесь в режиме командной строки и запустите Wdeb386.ехе. Типичная команда для его загрузки выглядит следующим образом: wdeb386.exe/c:1 /r:9600/s:myfite.sym/s:gdi.sym\windows\win.com.
/b> НУ Приложение А. Отладка
После запуска отладчика загружается Windows, и вы можете тестировать свое приложение. Чтобы перейти в отладчик, нажмите Ctrl+C на терминале или Ctrl+Alt+SysRq на основном компьютере. Если на вашем ПК имеется переключатель NMI (немаскируемого прерывания), он также может использоваться для выхода в отладчик. После этого ваш основной компьютер блокируется до выполнения очередной команды отладчика. Если вы не знаете, что делать дальше, попробуйте команду д — сокращение от go.
Команды для загрузки многочисленных символьных файлов удобно собрать в одном текстовом файле:
/s DDRAW16.SYM /s D3DRAMPF.SYM /s D3DRGBF.SYM /s KRNL386.SYM /S D3DRM8F.SYM /s GDI.SYM /s D3DRM16F.SYM /s D3DRG8F.SYM /s D3DRG16F.SYM /s D3DHALF.SYM
Сохраните этот список в файле, например Debug, inf. Затем можно создать простой пакетный файл для запуска сеанса отладки или ввести следующую командную строку:
wdeb386.exe c:l /r:9600 /f:debug.inf \windows\win.corn /
Подробные инструкции по работе с отладчиком приведены в руководстве пользователя Wdeb386, входящем в Win32 SDK.
Я бы купил эту книгу
Введение
Я бы купил эту книгу по следующим причинам:
• В ней содержится множество программ-примеров.
• Все программы написаны на C++.
• К книге прилагается библиотека, с которой можно легко экспериментировать.
• Все примеры были разработаны в среде Microsoft Visual C++ 4.0.
• В середине книги имеется красивая цветная вкладка.
• Автор встречался с представителями команды, разработавшей Direct3D.
• К книге прилагается полный комплект разработчика DirectX™ 2 Software Development Kit (SDK).
• Некоторые из представленных здесь идей можно воплотить в играх.
• Некоторые ее примеры не имеют отношения к играм.
• Мне больше не на что тратить деньги.
Я бы не стал покупать эту книгу по следующим причинам:
• В ней нет ни одной программы на ассемблере.
• Она не похожа на научный справочник.
• Книга слишком тонкая, чтобы ее можно было подложить под ножку обеденного стола.
• К ней не прилагаются стереоскопические очки.
• У меня уже есть такая книга.
Что вы узнаете из этой книги
Создавая эту книгу, я хотел показать вам, как написать трехмерное приложение для Microsoft Windows 95. Конечно, я не могу предоставить все примеры программ или описания библиотечных функций, которые обязательно понадобятся вам в будущем. Вместо этого я хочу научить вас самостоятельно решать нужную задачу, пользуясь документацией к DirectX 2 SDK и другими справочными материалами по программированию для Windows. Библиотека классов и примеры программ на прилагаемом диске CD-ROM содержат все, что вам может понадобиться для немедленного написания своего первого трехмерного приложения.
Немного истории
До недавнего времени все были уверены, что земля плоская. Это было очень удобно и для картографов, и для моряков. Первые могли нарисовать точное представление земной поверхности на листке бумаги и при этом не забывали предупредить о том, как опасно приближаться к краю. Вторым легко было разбираться в плоских картах плоского мира. Разумеется, моряки предпочитали держаться подальше от краев, на тот случай, если карта окажется неточной. С развитием вычислительной техники моряки стали переносить карты в память своих компьютеров. Хотя компьютеры времен Христофора Колумба еще не имели экранов высокого разрешения и работали как минимум от двух автомобильных
10 ДУ Введение
Немного истории '•fl 11

ции, встроенным в операционную систему. Все готово для создания приложений Windows, работающих с трехмерными объектами; остается лишь понять, как это делается, чему и посвящена настоящая книга.
Разработка трехмерных приложений
Примеры для этой книги создавались на компьютере Dell OptiPlex GXM 5120 с 32 Мб памяти и операционной системой Microsoft Windows 95. Использовались Microsoft Visual C++ 4.0 и DirectX 2 SDK. Я написал весь свой код на C++, а для компиляции и построения приложений применял библиотеки Microsoft Foundation Classes (MFC). Сочетание C++ с MFC позволило мне быстро создать «скелет» приложения, с которым можно было экспериментировать дальше. Я разработал комплект классов C++, инкапсулирующих функции механизма визуализации и облегчающих работу с ними. В этой книге мы рассмотрим разработанные мной классы, научимся использовать и расширять их для ваших собственных целей.
Если вы умеете программировать на С, но еще не перешли на C++ — вот вам отличный повод сделать это! Мой собственный опыт работы с C++ не так уж велик, и примеры будут понятны любому программисту на С, которому в течение нескольких недель пришлось иметь дело с C++. Если же вы не программируете на С, то советую вам вообще пропустить знакомство с ним и сразу начать с C++.
Я разрабатывал свои приложения и классы C++ с чисто практической точки зрения. Другими словами, я попытался создать средства для решения конкретных задач, а не ряд бесконечных примеров для демонстрации тех или иных возможностей. Вы не найдете в моих примерах классов типа CDog, CLabrador или CAardvark. Это вовсе не означает, что мы пропустим большинство возможностей механизма визуализации — мы используем их в той степени, в какой они нужны нам для создания приложений. *
Если вы не знакомы с концепциями трехмерной графики, будет полезно ознакомиться с превосходными трудами, в которых подробно рассматривается эта тема. В качестве справочника я бы предложил «Computer Graphics Principles and Practice» by Foley, vanDam, Feiner and Hughes (Addison-Wesley, 1991) или, например, «3D Computer Graphics» by Glassner (Lyon & Burford, 1989). Впрочем, чтение этих справочных пособий необязательно — развлечений хватит и без них.*
В комплект DirectX 2 SDK входят интерфейсы прикладных программ Direct3D, Directlnput, DirectSound, Direct3Dsound, DirectDraw и DirectPlay. Мы будем пользоваться интерфейсами Direct3D, DirectDraw и Directlnput, однако обойдемся без DirectSound и DirectPlay. В некоторых приложениях используется звук; если на вашем компьютере установлена звуковая карта, то время от времени вы будете приятно удивлены. Интерфейс Direct3D на самом деле состоит из нескольких уровней, самый верхний из которых носит название «абстрактного режима» (Retained Mode). Под ним находится уровень, называемый «непосредственным режимом» (Immediate Mode), а еще ниже — драйверы устройств. Иногда
• Отечестпеипому читателю можно порекомендовать, например, кпт-у Е. В. Шикипа, А. В. Борсс-коиа ^Компьютерная графика. Динамика, реалистические изображения». М.: Диалог-МИФИ, 1995. — Примеч. перец.
ч «* ••'^^w? ,-,
1 2. W Введение
в тексте книги упоминается «механизм визуализации» (rendering engine). Я использую этот термин, подразумевая библиотеку DirectSD в целом, от уровня абстрактного режима до драйверов, а не только растровый генератор (rasterizer), относящийся к непосредственному режиму.
Стиль программирования
Не беспокойтесь, вы не услышите тирады о правильной расстановке отступов или о положении фигурных скобок; я лишь хочу сделать несколько замечаний, относящихся к примерам программ — это именно примеры, не претендующие на роль прототипа рабочей программы. Во многих случаях я упростил код, отказавшись от обработки ошибок и использовав вместо нее директиву ASSERT для осуществления runtime-проверки в отладочной версии. Подобный метод помогает быстро находить самые «глупые» ошибки и выделять те фрагменты, в которых следует производить более тщательную обработку ошибок. Кроме того, учтите, что runtime-исключения в примерах не обрабатываются вообще. Чаще всего исключения возникают при распределении памяти, а это может происходить при конструировании многих различных объектов C++. Следует заметить, что вызов ASSERT для указателей, созданных оператором new, оказывается бессмысленным, так как реализация new для библиотек MFC самостоятельно возбуждает исключение при нехватке памяти для размещения объекта. Итак, для наших целей можно считать, что оператор new всегда работает успешно.
Для обозначения типа переменных используется простая схема, которая берет начало в так называемой «венгерской нотации», применяемой фирмой Microsoft. Мой собственный вариант выглядит несколько проще. В приведенной ниже таблице перечислены используемые префиксы и соответствующие им типы. Время от времени вам могут встретиться и другие префиксы — в таблице приведены наиболее распространенные.
Префикс
Тип
1
d
Р
Pi
m
int
double
Указатель
Указатель на СОМ-интерфейс
Член класса C++
Если вы относитесь к ветеранам программирования для Windows, то наверняка помните ненавистные указатели NEAR и FAR, которые использовались до перехода на 32-разрядные системы. Во многие структуры данных и прототипы функций Windows входят элементы с префиксом 1р, который означает «длинный (или дальний) указатель» (long pointer). Все указатели в моих программах — это просто указатели, и, соответственно, я пользуюсь только одним префиксом — р. Обычно я храню числа в переменных типа int и избегаю длинных целых типов. Если мне нужно значение с плавающей точкой, я всегда использую тип double. При этом расходы на хранение оказываются несколько выше, чем для float, но зато при вызове математических функций удается избежать приведения типа, генерируемого компилятором.
Стиль программирования ^Щ 13
Как видите, я использую несколько упрощенный подход к типам данных, который хорошо служит мне и помогает упростить программы. Разумеется, вы можете делать все, что захотите. Я не собираюсь приучать вас к своему стилю работы. Мое скромное желание — чтобы вы разобрались в моих программах.
Библиотека SdPlus
Существует несколько методик построений примеров, которые эволюционируют по мере изложения материала в книге. Первый вариант — включать в каждый пример лишь тот код, который необходим для текущего уровня понимания читателя. Затем весь код из одного примера копируется в другой и к нему добавляются новые фрагменты. Мне нравится этот подход, которым я воспользовался в своей книге «Animation Techniques in Win32», поскольку там можно было точно определить, какие познания необходимы для понимания примера в каждый конкретный момент.
Тем не менее в этой книге я решил поступить с примерами иначе — с самого начала представлять читателю практически весь код, а потом детально рассматривать только те фрагменты, которые необходимы для каждого примера. Я выбрал такой подход, поскольку для создания даже самого первого примера требуется достаточно большой объем кода. Хотя ничего лишнего в нем нет, на самом деле вам не обязательно с самого начала знать, как все это работает (кроме того, использование единой кодовой основы во всех примерах сокращает вероятность появления мелких ошибок). Я разработал библиотеку, содержащую общий код для всех моих примеров: библиотеку 3dPlus.
Если вас беспокоит производительность работы приложения с большим объемом кода на C++, позвольте вас заверить, что прослойка C++ на самом деле очень тонка. Во многих случаях устанавливается прямое соответствие между вызовом функции класса C++ и обращением к функции СОМ-интерфейса Direct3D;
если пожелаете, можно обойти прослойку C++ и работать напрямую с интерфейсом Direct3D. На самом деле, по мере развития вашего приложения, вы непременно придете к выводу, что в моей библиотеке реализованы не все необходимые функции. В этом случае можно либо самостоятельно расширить библиотеку, либо непосредственно обращаться к интерфейсу Direct3D.
Интерфейс Direct3D
Система Direct3D построена на основе СОМ — составной объектной модели (Component Object Model), технологии, которая используется фирмой Microsoft при создании операционной системы следующего поколения (кодовое наименование Cairo). Direct3D — одно из первых дополнений Windows, использующее эту технологию, если не считать подсистемы связывания и внедрения объектов (OLE). СОМ-объекты при программировании на C++ играют ту же роль, что и библиотеки динамической компоновки (DLL) при программировании для Windows на языке С. Это не значит, что СОМ-объекты могут использоваться только в приложениях, написанных на C++; скорее речь идет о том, что СОМ-объекты предоставляют хорошую основу для создания системных компонентов. Кроме того, они прекрасно уживаются с программами на C++.
В СОМ- объектах используется таблица указателей на их функции, которая обычно называется v-таблицей (vtable). Аналогичный механизм задействован и в C++ для реализации виртуальных функций класса. Подобно тому, как функции
14 Введение
C++ вызываются из программы на С ценой минимальных дополнительных усилий, можно обращаться к интерфейсам СОМ-объектов из программы на С. Работа с интерфейсами СОМ-объектов из программы на С облегчается тем, что она происходит аналогично работе с функциями классов C++. Фрагмент программы на С, в котором встречается обращение к интерфейсу СОМ-объекта, выглядит следующим образом:
pInterface->lpVtbl->Member(pinterface, argi) ;
А вот как выглядит тот же самый фрагмент в программе на C++:
pInterface->Member(argi) ;
Для определения «срока жизни» СОМ-объектов используются счетчики обращений. Когда на СОМ-объект не остается ни одной ссылки, он сам себя уничтожает. Этот простой механизм заметно облегчает совместное использование СОМ-объектов и освобождает программиста от разнообразных хлопот по управлению данными. Тем не менее это означает, что для правильного использования объектов вы должны представлять себе работу механизма подсчета ссылок.
По сути дела каждый раз, когда СОМ-объект возвращает вам указатель на один из своих интерфейсов, он наращивает значение своего счетчика обращений. Копируя указатель на интерфейс, необходимо нарастить значение счетчика обращений вызовом функции AddRef. После завершения работы с указателем следует вызвать функцию Release данного интерфейса, чтобы уменьшить значение счетчика обращений. На самом деле этим дело не ограничивается, но основная суть именно такова. Приведу фрагмент программы на C++, который получает указатель на интерфейс СОМ-объекта, вызывает функцию интерфейса и затем освобождает его:
pinterface = GetSomeCOMInterface() ;
pInterface->CallMember() ;
p!nterface->Release() ;
Обратите внимание на то, что после вызова Release значением указателя пользоваться уже нельзя, так как объект, на который он ссылается, может оказаться уничтоженным (если вы освободили последнюю или единственную копию объекта). Обычно после вызова Release я присваиваю указателю значение NULL, чтобы облегчить поиск программных ошибок — например, попыток использования недопустимого указателя па интерфейс. Если вы любите макросы (лично я их не люблю), то всегда можете создать макрос RELEASE, который вызывает функцию Release и присваивает указателю значение NULL:
ftdefine RELEASE(p) ((р)->Release(); (p)=NULL;)
Я подумал, что изучение технологии трехмерного программирования — и так непростая задача, поэтому «спрятал» СОМ-интерфейсы DirectSD внутри классов библиотеки 3dPlus, написанных на C++. Если вы привыкнете к библиотечным функциям DirectSD, то можете ничего не знать о лежащих в ее основе СОМ-интерфейсах. Но если вы захотите расширить библиотеку или программировать, не пользуясь библиотечными функциями, вам придется познакомиться с работой СОМ-объектов. Ниже мы рассмотрим многие интерфейсы Direct3D,
Интерфейс DirectSD 'в¦ 15
поэтому к концу книги вы будете хорошо представлять себе их работу, независимо от того, собираетесь ли вы непосредственно использовать их или нет.
Если вы хотите больше узнать о СОМ-объектах, рекомендую прочитать книгу «Inside OLE» (second edition), Kraig Brockschmidt, или многочисленные статьи, входящие в Microsoft Developer Library.
Несколько последних замечаний
Знакомясь с примерами программ в тексте книги, вы обычно сможете отличить обращения к объектам библиотеки 3dPlus от обращении к механизму визуализации по именам объектов. Если имя выглядит как С3с)<имя>, то объект относится к классу C++ и является членом библиотеки 3dPlus. Если вы увидите С<имя>, то ire исключено, что объект также входит в библиотеку 3dPlus (или относится к библиотеке MFC), но более вероятно, что перед вами объект C++, созданный всего для одного примера. Если же вы увидите 1<имя>, то это интерфейс, который так или иначе относится к библиотеке Direct3D. Любой указатель, который начинается с р1<имя>, является указателем на интерфейс Direct3D.
При запуске приложений-примеров вы, вероятно, обратите внимание на то, что многие из них имеют черный фон. В книге для удобства используется белый цвет фона.
Работа с диском CD-ROM
Прилагаемый к книге диск содержит примеры приложений, которые демонстрируют изложенные в книге концепции. Вы можете обращаться к файлам приложений прямо на диске, но я бы посоветовал воспользоваться программой Setup для копирования файлов па жесткий диск, где вы сможете поэкспериментировать с ними, модифицировать и использовать их как основу для создания ваших собственных приложений (для этого потребуется примерно 45 Мб дискового пространства). Запустите Setup.exe и следуйте инструкциям на экране. Все примеры приложений копируются на ваш жесткий диск, в каталог \3D (если только вы не изменили каталог, принятый по умолчанию). На диск переносится структура каталогов с примерами, все необходимые файлы для построения и запуска приложений, выполняемые файлы, а также файлы рабочей области проектов (MDP).
Кроме того, в каталоге \MSDX2SDK на диске CD-ROM находится DirectX 2 SDK, a в каталоге \Tools — некоторые утилиты, которые могут пригодиться при трехмерном программировании. В SDK имеется отдельная программа Setup, которую необходимо запустить, а утилиты из каталога Tools можно скопировать вручную в случае необходимости.
Мелким шрифтом
Мои программы никогда не бывают идеальными, а мои подход к решению проблемы может не совпадать с предложенным вами. Кроме того, несмотря на все мои усилия, текст книги, вероятно, содержит опечатки. Если вы найдете какие-либо ошибки или захотите внести предложения, пожалуйста, сообщите мне. Я не обещаю решить за вас все проблемы, но постараюсь конструктивно ответить на все полученные сообщения.
Мой адрес электронной почты: nigel-t@msn.combusy. Найджел Томпсон, 1996 год.
Выражение признательности
Выражение признательности
При создании этой книги я получил незначительную помощь от большого количества людей и большую помощь — от незначителвного числа людей. Хочу поблагодарить всех, кто отдал книге свое время и силы (надеюсь, я никого не забуду).
Эрик Стру (Eric Stroo) пригласил меня на демонстрацию Direct3D, проводимую Кент Сикингс (Kate Seekings); именно это событие и вдохновило меня на написание книги.
Дуг Рэбсон (Doug Rabson), Стив Лэйси (Steve Lacey), Джайлс Берджесс (Giles Burgess) и Серван Кеонджиан (Servan Keondjian) из команды программистов Direct3D оказали техническую поддержку по механизму визуализации. Особенно хочется поблагодарить Дуга Рэбсона за ответы, которые он давал на сотни моих вопросов по электронной почте, даже во время выпуска различных бета-версий.
Майкл Виктор (Michael Victor) создал многие трехмерные объекты, использованные в качестве примеров, и превратил наброски автора в полноценные диаграммы.
Мои редакторы Эверилл Карди (Averill Curdy), Джин Росс (Jean Ross) и Виктория Талман (Victoria Thulman), а также все остальные хорошие люди из Microsoft Press помогали мне в работе над книгой.
Дейл Роджерсон (Dale Rogerson) прервал работу над своей книгой, чтобы составить рецензию на мою.
Сердечно благодарю Нэнси Клатс (Nancy Cluts), которая выделила время, чтобы построить и протестировать некоторые примеры, а также написала подробные рецензии по всем главам.
Столь же сердечно благодарю и Ричарда Норена (Richard Noren) за его чрезвычайно подробные рецензии по главам.
Я признателен и многим другим людям, которые помогали мне в написании книги. Среди них: Дон Сперэй (Don Speray), Эрик Берридж (Eric Berridge), Грег Бинкерд (Greg Binkerd), Хан X. Нгуен (Hung H. Nguyen), Джефф В. Стоун (Jeff W. Stone), Джим Блинн (Jim Blinn), Марк Гендрон (Mark Gendron), Майкл Мэлоун (Michael Malone), Пол Дэвид (Paul David), Стив Лэйси (Steve Lacey) и Сью Леду (Sue Ledoux). Спасибо всем!
Благодарю Ричарда Грэншоу (Richard Granshaw) за помощь в особенно сложных ситуациях, которые возникали при работе с моим вариантом Direct3D.
Благодарю фирму Spacetec IMC Corporation за подаренный мне Spaceball Avenger.
Благодарю Денниса Крейна (Dennis Crain), которому во время написания книги я мог пожаловаться на свои проблемы и на жизненные тяготы в целом.
Наконец, хочу поблагодарить свою жену Тамми: за то, что она убедила меня, будто я смогу написать эту книгу в несуществующее свободное время, и помогала мне, отвлекая на себя наших троих детей, Рона, Нелл и Марка; за то, что она периодически просовывала пищу под мою дверь; и за то, что не слишком много жаловалась, хотя в процессе написания книги снова забеременела. Я тебя люблю.