Алгоритмы упорядочения

Упорядочение — это еще одна характерная для разреженных матриц операция. Ее алгоритм

реализуется несколькими функциями:

• р = colmmd(S) — возвращает вектор упорядоченности столбцов разреженной матрицы S. [то nzmax(S) — максимальное количество ячеек для хранения ненулевых элементов. Если S — полная матрица, то nzmax(S)=numel(S).] Для несимметрической матрицы S вектор упорядоченности столбцов р такой, что S(:. р) будет иметь более разреженные L и U в LU-разложении, чем S. Такое упорядочение автоматически применяется при выполнении операций обращения \ и деления /, а также при решении систем линейных уравнений с разреженными матрицами. Можно использовать команду spparms, чтобы изменить некоторые параметры, связанные с эвристикой в алгоритме colmmd;
• j = colperm(S) — возвращает вектор перестановок j, такой что столбцы матрицы S(:. j) будут упорядочены по возрастанию числа ненулевых элементов. Эту функцию полезно иногда применять перед выполнением LU-разложения. Если S — симметрическая матрица, то j=colperm(S) возвращает вектор перестановок j, такой что и столбцы, и строки S(j,j) упорядочены по возрастанию ненулевых элементов. Если матрица S положительно определенная, то иногда полезно применять эту функцию и перед выполнением разложения Холецкого.

Пример:

» S=sparse([2.3.1.4.2].[l,3.2.3.2],[4.3,5.6.7].4.5);full(S) 

ans =

0    5    0    0    0

4    7    0    0    0

0    0    3    0    0

0    0    6    0    0 

» t=colperm(S)

t=
	5	1	2	3
»full(S(;,t))
ans =
0	0	0	5	0
0	0	4	7	0
0	0	0	0	3
0	0	0	0	6

• p = dmperm(A) — возвращает вектор максимального соответствия р такой, что если исходная матрица А имеет полный столбцовый ранг, то А(р.:) — квадратная матрица с ненулевой диагональю. Матрица А(р,:) называется декомпозицией Далмейджа-Мендельсона, или DM-декомпозицией.

Если А — приводимая матрица, [ Квадратная матрица А называется приводимой, если она подобна клеточной матрице, квадратные элементы которой соответствуют индукции линейного оператора А в отдельные подпространства. — Примеч. ред. ]  линейная система Ах=b может быть решена приведением А к верхней блочной треугольной форме с неприводимым диагональным блоком. Решение может быть найдено методом обратной подстановки.

• [p.q.r] = dmperm(A) — находит перестановку строк р и перестановку столбцов q квадратной матрицы А, такую что A(p,q) — матрица в блоке верхней треугольной формы.

Третий выходной аргумент г — целочисленный вектор, описывающий границы блоков. К-й блок матрицы A(p,q) имеет индексы r(k):r(k+l)-l.

• [p.q.r.s] = dmperm(A) — находит перестановки р и q и векторы индексов г и s, так что матрица A(p,q) оказывается в верхней треугольной форме. Блок имеет индексы (r(i):r(i+l)-l,s(i):s(i+l)-l).

В терминах теории графов диагональные блоки соответствуют сильным компонентам Холла графа смежности матрицы А.

Примеры:

» A=sparse([1.2,1.3.2].[3.2.1.1.1].[7.6,4.5,4],3,3)

:full(A) 

ans =

4 0 

4 6 0

5 0 0   

»[p.q.r]=dmperm(A)

Р=

1 2 3

q =

3 2 1 

r =

1 2 3 4 

» fulKA(p.q)) 

ans =

7 0 4

0 6 4

0 0 5

• symmmd(S) — возвращает вектор упорядоченности для симметричной положительно определенной матрицы S, так что S(p,p) будет иметь более разреженное разложение Холецкого, чем S. Иногда symmmd хорошо работает с симметрическими неопределенными матрицами. Такое упорядочение автоматически применяется при выполнении операций \ и /, а также при решении линейных систем с разреженными матрицами [ Функция symamd работает значительно быстрее. — Примеч. ред. ].  

Можно использовать команду spparms, чтобы изменить некоторые опции и параметры, связанные с эвристикой в алгоритме.

Алгоритм упорядочения для симметрических матриц основан на алгоритме упорядочения по разреженности столбцов. Фактически symmmd(S) только формирует матрицу К с такой структурой ненулевых элементов, что К' *К имеет тот же трафик разреженности, что и S, и затем вызывает алгоритм упорядочения по разреженности столбцов для К. На рис. 12.2 приводится пример применения функции symmmd к элементам разреженной матрицы.

Пример:

» B=bucky;p=symmmd(B);

» R=B(p,p);

» subplot(1,2,1),spy(B); subplot(1,2,2).spy(R) ;

•  r = symrcm(S) — возвращает вектор упорядоченности для симметричной матрицы S и называется упорядочением Катхилла-Макки. Причем формируется такая перестановка г, что S(r.r) будет концентрировать ненулевые элементы вблизи диагонали. Это хорошее упорядочение как перед LU-разложением, так и перед разложением Холецкого. Упорядочение применимо как для симметрических, так и для несимметрических матриц.

Для вещественной симметрической разреженной матрицы S (такой, что S=S ^T ) собственные значения S(r.r) совпадают с собственными значениями S, но для вычисления eig(S(r,r)) требуется меньше времени, чем для вычисления eig(S).

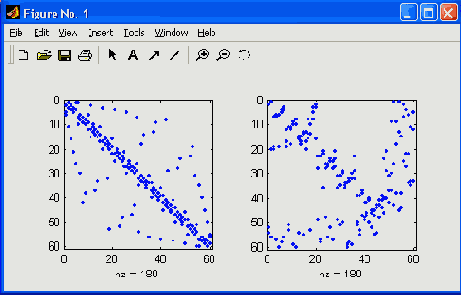
Рис. 12.2. Пример применения функции symmmd

Пример:

» B=bucky;p=symrcm(B);

» R=B(p,p);

» subplot(1,2,1),spy(B);subplot(1,2,2),spy(R) ;

На рис. 12.3 приведен пример концентрации ненулевых элементов разреженной матрицы вблизи главной диагонали.

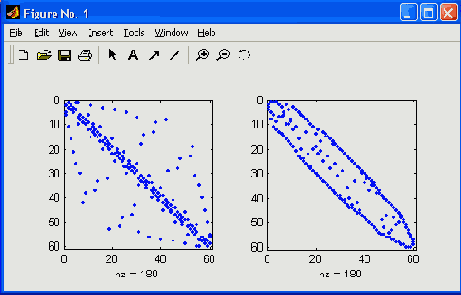
Рис. 12.3. Пример применения функции symrcm

 

Содержание раздела

---

---