Элементарные средства решения СЛУ

Решение систем линейных уравнений (СЛУ) относится к самой массовой области применения матричных методов, описанных в уроках 10-12. В этом разделе вы найдете ответы на вопросы,

каким образом применяются указанные методы и какие дополнительные функции имеет система MATLAB для решения систем линейных уравнений.

Как известно, обычная СЛУ имеет вид:

а ₁₁ X ₁ , а ₁₂ ,X ₂ ..., а _1n X _n =b ₁

Здесь а ₁₁ , а, ₂ ,..., а _пп — коэффициенты, образующие матрицу А, которые могут иметь действительные или комплексные значения, x ₁ , х ₂ ,..., х _п — неизвестные, образующие вектор X, и b ₁ , b ₂ ,..., b _п — .свободные члены (действительные или комплексные), образующие вектор В. Эта система может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений, X — искомый вектор неизвестных и В — вектор свободных членов. В зависимости от вида матрицы А и ее характерных особенностей MATLAB позволяет реализовать различные методы решения.

Для реализации различных алгоритмов решения СЛУ и связанных с ними матричных операций применяются следующие операторы: +,-,*,/, \, *, ' . Как отмечалось ранее, MATLAB имеет два различных типа арифметических операций — поэлементные и для массивов (векторов и матриц) в целом. Матричные арифметические операции определяются правилами линейной алгебры.

Арифметические операции сложения и вычитания над массивами выполняются поэлементно. Знак точки «.» отличает операции над элементами массивов от матричных операций. Однако, поскольку операции сложения и вычитания одинаковы для матрицы и элементов массива, знаки «.+» и «.-» не используются. Рассмотрим другие операторы и выполняемые ими операции.

* — матричное умножение;
С = А*В — линейное алгебраическое произведение матриц А и В:

Для случая нескалярных А и В число столбцов матрицы А должно равняться числу строк матрицы В. Скаляр может умножаться на матрицу любого размера.

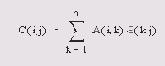
/ — правое деление. Выражение Х=В/А дает решение ряда систем линейных уравнений АХ=В, где А — матрица размера тхп и В — матрица размера nxk;
\ — левое деление. Выражение Х=В\А дает решение ряда систем линейных уравнений ХА=В, где А — матрица размера тхп и В — матрица размера nxk. Если А — квадратная матрица, то А\В — примерно то же самое, что и inv(A)*B, в остальных случаях возможны варианты, отмеченные ниже.

Если А — матрица размера пхп, а В — вектор-столбец с п компонентами или матрица с несколькими подобными столбцами, тогда Х=А\В — решение уравнения АХ=В, которое находится хорошо известным методом исключения Гаусса.

Если А — матрица размера тхп и тхп, а В представляет собой вектор-столбец с m компонентами или матрицу с несколькими такими столбцами, тогда система оказывается недоопределенной или переопределенной и решается на основе минимизации второй нормы невязок.

Ранг k матрицы А находится на основе QR-разложения (урок 11) с выбором ведущего элемента. Полученное решение X будет иметь не больше чем k ненулевых компонентов на столбец. Если k<n, то решение, как правило, не будет совпадать с pinv(A)*B, которое имеет наименьшую норму невязок ||Х||.

^ — возведение матрицы в степень. Х ^А р — это X в степени р, если р — скаляр. Если р — целое число, то степень матрицы вычисляется путем умножения X на себя р раз. Если р — целое отрицательное число, то X сначала инвертируется. Для других значений р вычисляются собственные значения и собственные векторы, так что если [V.D]=eig(X), то X*p=V*D. ^A p/V. Если X — скаляр и Р — матрица, то Х ^А Р — это скаляр X, возведенный в матричную степень Р. Если X и Р — матрицы, то Х ^Л Р становится некорректной операцией и система выдает сообщение об ошибке. Возможный вариант решения матричного уравнения АХ=В с применением оператора ^{^} можно представить как Х=В*А ^{^} -1.
' — транспонирование матрицы, то есть замена строк столбцами и наоборот. Например, А' — транспонированная матрица А. Для комплексных матриц транспонирование дополняется комплексным сопряжением. Транспонирование при решении СЛУ полезно, если в матрице А переставлены местами столбцы и строки.

При записи СЛУ в матричной форме необходимо следить за правильностью записи матрицы А и вектора В. Пример (в виде m-файла):


А-[2 1	0	1:
1 -3	2	4;
-5 0	-1	-7:
1 -6	2	6]:
В=[8 9	-5	0]:
Х1=В/А
Х2=В*А ^{^} -1
X3=B*inv(A)

Эта программа выдает результаты решения тремя способами:

X1 =

3.0000 -4.0000-1.00001.0000

Х2 =

3.0000 -4.0000-1.00001.0000

X3 =

3.0000 -4.0000-1.00001.0000

Как и следовало ожидать, результаты оказываются одинаковыми для всех трех методов. При решении систем линейных уравнений, особенно с разреженной матрицей коэффициентов, полезно применение функций colmmd (colamd), symmmd (symamd), описанных ранее в уроке 12.

Содержание раздела