Численное интегрирование методом квадратур

Приведенные ниже функции осуществляют интегрирование и двойное интегрирование, используя квадратурную формулу Симпсона или метод Гаусса-Лобатто. Квадратура — численный метод нахождения площади под графиком функции/(т), т. е. вычисление определенного

интеграла вида

В приведенных ниже формулах подынтегральное выражение fun обычно задается в форме дескриптора функции, поэтому с дидактическими целями используем нотацию @fun.

Функции quad и quadl используют два различных алгоритма квадратуры для вычисления определенного интеграла. Функция quad выполняет интегрирование по методу низкого порядка, используя рекурсивное правило Симпсона [4, 40]. Но она может быть более эффективной при негладких подынтегральных функциях или при низкой требуемой точности вычислений. Алгоритм quad в MATLAB 6 изменен по сравнению с предшествовавшими версиями, точность по умолчанию по сравнению с версиями 5.3х повышена в 1000 раз (с 10- ³ до 10- ⁶ ). Новая функция quadl (квадратура Лобатто) использует адаптивное правило квадратуры Гаусса— Лобатто очень высокого порядка. Устаревшая функция quads выполняла интегрирование, используя квадратурные формулы Ньютона—Котеса 8-го порядка [40]. Достижимая точность интегрирования гладких функций в MATLAB 6 поэтому также значительно выше, чем в предшествующих версиях.

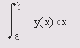
quad(@fun,a.b) — возвращает численное значение определенного интеграла от заданной функции @fun на отрезке [а Ь]. Используется значительно усовершенствованный в MATLAB 6 адаптивный метод Симпсона;
quad(@fun,a.b.tol) — возвращает численное значение определенного интеграла с заданной относительной погрешностью tol. По умолчанию to1=l.e-6. Можно также использовать вектор, состоящий из двух элементов tol =[rel_tol abs_tol], чтобы точно определить комбинацию относительной и абсолютной погрешности;
quad(@fun,a.b,tol .trace) — возвращает численное значение определенного интеграла и при значении trace, не равном нулю, строит график, показывающий ход вычисления интеграла;
quad(@fun,a,b.tol,trace,PI,P2,...) — возвращает численное значение определенного интеграла по хот подынтегральной функции fun, использует дополнительные аргументы P1, P2,..., которые напрямую передаются в подынтегральную функцию: G=fun(X.Pl,P2,...). Примеры:

» quad('(exp(x)-l)',0,1,1e-5)

ans =

0.7183

» q = quad(@exp,0,2,1e-4)

q =

6.3891

» q = quad(@sin.0,pi,le-3)

q = 2.0000

dblquad(@fun,inmin,inmax.outmin,outmax) — вычисляет и возвращает значение двойного интеграла для подынтегральной функции fun (Inner, outer), по умолчанию используя квадратурную функцию quad. Inner — внутренняя переменная, изменяющаяся на закрытом интервале от inmin до inmax, a outer — внешняя переменная, изменяющаяся на закрытом интервале от outmin до outmax. Первый аргумент @fun — строка, описывающая подынтегральную функцию. Этс может быть либо дескриптор функции, либо объект inline (в последнем случае символ «@» в ее записи отсутствует). Обычная запись в апострофах тепер недопустима. Эта функция должна быть функцией двух переменных вид. fout=fun(inner.outer). Функция должна брать вектор inner и скаляр outer возвращать вектор fout, который является функцией, вычисленной в outer и каждом значении inner [ Функция inime('expr', 'argl',...'argn') так же создает объект, но без дескриптора, 'ехрг' — выражеши Строки 'argx' —входные аргументы. При их отсутствии по умолчанию подставляется х. Если вмест 'arg' — скаляр, то он означает количество дополнительных переменных Р. Примеры запис; g = inline(exp); g - inline('t ^A 2'); g = inline('sin(2*pi*f + theta)'); g = inline('sin(2*pi*f + theta)', : 'theta'); g - inline('x ^A Pl+P2', 2). - Примеч. ред. ];
dblquad(@fun,inmin.inmax.outmin,oiitmax,tol .trace) — передает в функцию dblquad параметры tol и trace. Смотрите справку по функции quad для получения информации о параметрах to! и trace;
dblquad(@fun,inmin,inmax,outmin,outmax.tol .trace,order) — передает параметры tol и trace для функции quad или quadl в зависимости от значения строки order. Допустимые значения для параметра order — @quad , @quadl или имя любого определенного пользователем квадратурного метода с таким же вызовом и такими же возвращаемыми параметрами, как у функций quad и quad!. (Например, при проверке старых программ можно использовать @quad8 для большей совместимости с прежними версиями MATLAB). По умолчанию (без параметра order) вызывается @quad. поскольку подинтегральные функции могут быть негладкими.

Пример: пусть m-файл integl.m описывает функцию 2*y*sin(x)+x/2*cos(y), тогда вычислить двойной интеграл от той функции можно следующим образом:

» result = dblquad(@integl,pi,2*pi,0.2*pi)

result =

78.9574

Содержание раздела