Функции одномерного прямого преобразования Фурье

В описанных ниже функциях реализован особый метод быстрого преобразования Фурье — Fast

Fourier Transform (FFT, или БПФ), позволяющий резко уменьшить число арифметических операций в ходе приведенных выше преобразований. Он особенно эффективен, если число обрабатываемых элементов (отсчетов) составляет 2 ^т , где т — целое положительное число. Используется следующая функция:

fft(X) — возвращает для вектора X дискретное преобразование Фурье, по возможности используя алгоритм быстрого преобразования Фурье. Если X — матрица, функция fft возвращает преобразование Фурье для каждого столбца матрицы;
fft(X.n) — возвращает n-точечное преобразование Фурье. Если длина вектора X меньше n, то недостающие элементы заполняются нулями. Если длина X больше п, то лишние элементы удаляются. Когда X — матрица, длина столбцов корректируется аналогично;
fft(X,[ Ldirn) и fft(X,n,dim) — применяют преобразование Фурье к одной из размерностей массива в зависимости от значения параметра dim.

Для иллюстрации применения преобразования Фурье создадим трехчастотный сигнал на фоне сильного шума, создаваемого генератором случайных чисел:

»t=0:0.0005:1;

»x=sin(2*pi*200*t)+0.4*sin(2*pi*150*t)

+0.4*sin(2*pi*250*t);

» y=x+2*randn(size(t));

» plot(y(1:100),'b')

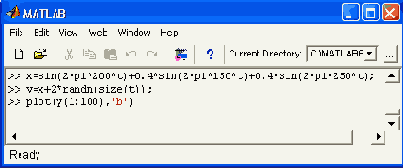
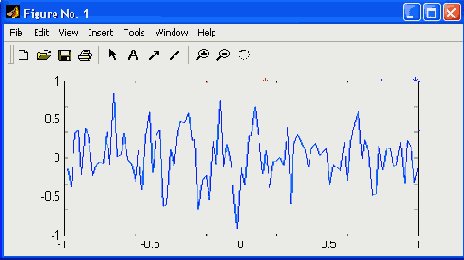
Рис. 17.6. Форма зашумленного сигнала

Этот сигнал имеет среднюю частоту 200 рад/с и два боковых сигнала с частотами 150 и 250 рад/с, что соответствует амплитудно-модулированному сигналу с частотой модуляции 50 рад/с и глубиной модуляции 0.8 (амплитуда боковых частот составляет 0.4 от амплитуды центрального сигнала). На рис. 17.6 показан график этого сигнала (по первым 100 отсчетам из 2000). Нетрудно заметить, что из него никоим образом не видно, что полезный сигнал — амплитудно-модулированное колебание, настолько оно забито шумами. Теперь построим график спектральной плотности полученного сигнала с помощью прямого преобразования Фурье, по существу переводящего временное представление сигнала в частотное. Этот график в области частот до 300 Гц (см. рис. 17.6) строится с помощью следующих команд:

» Y=fft(y,1024):

» Pyy=Y.*conj(Y)/1024;

» f=2000*(0:150)/1024;

» plot(f,Pyy(l:151)),grid

График спектральной плотности сигнала, построенный в этом примере, представлен на рис. 17.7. Даже беглого взгляда на рисунок достаточно, чтобы убедиться в том, что спектрограмма сигнала имеет явный пик на средней частоте амплитудно-модулированного сигнала и два боковых пика. Все эти три частотные составляющие сигнала явно выделяются на общем шумовом фоне. Таким образом, данный пример наглядно иллюстрирует технику обнаружения слабых сигналов на фоне шумов, лежащую в основе работы радиоприемных устройств.

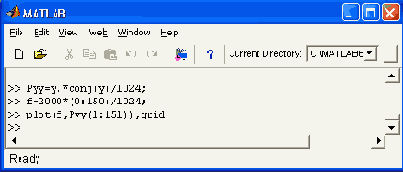
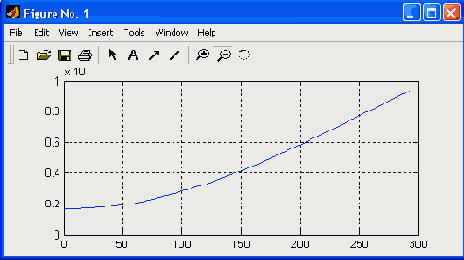
Рис. 17.7. График спектральной плотности приведенного на рис. 17.6 сигнала

Содержание раздела