Матричная лаборатория MatLab
Полиномиальная регрессия
Одна из наиболее известных аппроксимаций — полиномиальная. В системе MATLAB определены функции аппроксимации данных полиномами по методу наименьших квадратов — полиномиальной регрессии. Это выполняет функция, приведенная ниже:-
polyfit(x.y.n)
— возвращает вектор коэффициентов полинома р(х) степени п, который с наименьшей
среднеквадратичной погрешностью аппроксимирует функцию у(х). Результатом
является вектор-строка длиной n+1, содержащий коэффициенты полинома в порядке
уменьшения степеней х и у равно n+1, то реализуется обычная полиномиальная
аппроксимация, при которой график полинома точно проходит через узловые
точки с координатами (х.у), хранящиеся в векторах х и у. В противном случае
точного совпадения графика с узловыми точками не наблюдается;
- [p.S] = polyflt(x.y.n) — возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предсказания погрешности;
- [p.S] = polyf1t(x,y,n,mu) возвращает коэффициенты полинома р и структуру S для использования вместе с функцией polyval с целью оценивания или предска-зния погрешности, но так, что присходит центрирование (нормирование) и масштабирование х, xnorm = (х - mu(l))/mu(2), где mu(l) = mean(x) и mu(2) = std(x). Центрирование и масштабирование не только улучшают свойства степенного многочлена, получаемого при помощи polyval, но и значительно повышают качественные характеристики самого алгоритма аппроксимации.
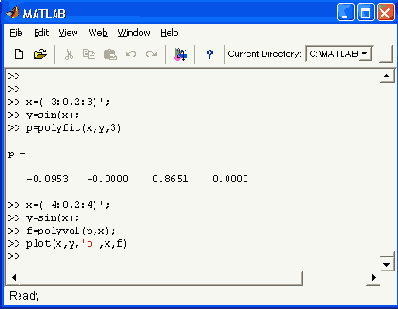
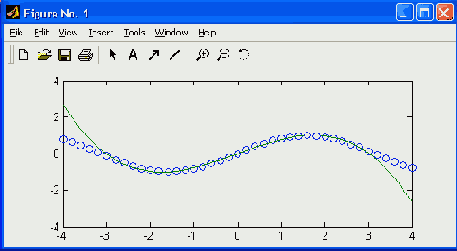
Рис. 17.10. Пример использования функции polyfit
Пример (полиномиальная регрессия для функции s » х=(-3:0.2:3)'; y=sin(x); p=polyflt(x,y,3) р = -0.0953 0.0000 0.8651 -0.0000 »x=(-4:0.2:4)';y=sin(x); » f=polyval(p,x);plot(x,y,'o',x,f) Рис. 17.14, построенный в этом примере, дает наглядное представление о точности полиномиальной аппроксимации. Следует помнить, что она достаточно точна в небольших окрестностях от точки х = 0, но может иметь большие погрешности за их пределами или в промежутках между узловыми точками. График аппроксимирующего полинома третьей степени на рис. 17.10 показан сплошной линией, а точки исходной зависимости обозначены кружками. К сожалению, при степени полинома свыше 5 погрешность полиномиальной регрессии (и аппроксимации) сильно возрастает и ее применение без центрирования и масштабирования становится рискованным. Обратите внимание на то, что при полиномиальной регрессии узловые точки не ложатся точно на график полинома, поскольку их приближение к нему является наилучшим в смысле минимального среднеквадратического отклонения. Об этом уже говорилось.