Интерполяция периодических функций рядом Фурье

Под интерполяцией обычно подразумевают вычисление значений функции f(x) в промежутках между

узловыми точками. Линейная, квадратичная и полиномиальная интерполяция реализуются при полиномиальной аппроксимации. А вот для периодических (и особенно для гладких периодических) функций хорошие результаты может дать их интерполяция тригонометрическим рядом Фурье. Для этого используется следующая функция:

interpft(x.n) — возвращает вектор у, содержащий значения периодической функции, определенные в п равномерно расположенных точках. Если length(x)=rr; и х имеет интервал дискретизации dx, то интервал дискретизации для у составляет dy=dx*m/n, причем п не может быть меньше, чем т. Если X — матрица, interpft оперирует столбцами X, возвращая матрицу Y с таким же числом столбцов, как и у X, но с п строками. Функция y=interpft(x.n.dim) работает либо со строками, либо со столбцами в зависимости от значения параметра dim.

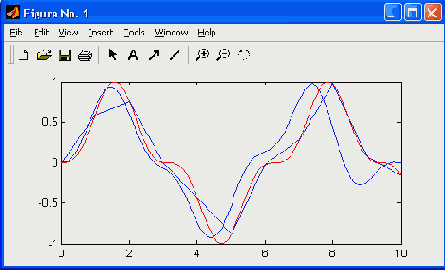
Рис. 17.11. Пример использования функции interpft

Пример:

» x=0:10; y=sin(x).^3;

» x1=0:0.1:10; y1=interpft(y,101);

» x2=0:0.01:10; y2=sin(x2).^3;

» plot(x1,y1, 'r').hold on.plot(x,y, 'b',x2,y2)

Рис. 17.11 иллюстрирует эффективность данного вида интерполяции на примере функции sin(x).^3, которая представляет собой сильно искаженную синусоиду.

Исходная функция на рис. 17.12 представлена сплошной линией с кружками, а интерполирующая функция — штрих-пунктирной линией.

Содержание раздела