Интерполяция на неравномерной сетке

Для интерполяции на неравномерной сетке используется функция griddata:

• ZI = griddata(x.y.z.XI.YI) — преобразует поверхность вида z = f(x. у), которая определяется векторами (x.y.z) с (обычно) неравномерно распределенными элементами. Функция griddata аппроксимирует эту поверхность в точках, определенных векторами (XI.YI) в виде значений ZI. Поверхность всегда проходит через заданные точки. XI и YI обычно формируют однородную сетку (созданную с помощью функции meshgrid).

XI может быть вектором-строкой, в этом случае он определяет матрицу с постоянными столбцами. Точно так же YI может быть вектором-столбцом, тогда он определяет матрицу с постоянными строками.

• [XI.YI.ZI] = griddata(x,y,z,xi ,yi ) — возвращает аппроксимирующую матрицу ZI, как описано выше, а также возвращает матрицы XI и YI, сформированные из вектора-столбца xi и вектора-строки yi . Последние аналогичны матрицам, возвращаемым функцией meshgrid;
• [...] = griddata (....method) — использует определенный метод интерполяции:
  • 'nearest' — ступенчатая интерполяция;
  • 'linear' — линейная интерполяция (принята по умолчанию);
  • 'cubic' — кубическая интерполяция;
  • ' v4 ' — метод, используемый в МATLAB 4.

Метод определяет тип аппроксимирующей поверхности. Метод 'cubic ¹ формирует гладкие поверхности, в то время как 'linear' и 'nearest' имеют разрывы первых и нулевых производных соответственно. Все методы, за исключением v4, основаны на триангуляции Делоне. Метод ' v4 ' включен для обеспечения совместимости с версией 4 системы MATLAB. Пример:

» x=rand(120.1)*4-2;y=rand(120.1)*4-2;

z=x,*y,*exp(-x.^2-y.^2); 

» t=-2:0.1:2;[X,Y]=meshgrid(t,t);

Z=griddata(x.y.z.X.Y); 

» mesh(X.Y.Z),hold on;plot3(x.y,z, 'ok')

Функции griddataS и griddatan работают аналогично griddata, но для для трехмерного и n-мерного случая — с использованием алгоритма qhul 1 . Используются, в частности, при трехмерной и n-мерной триангуляции.

Рис. 17.13 иллюстрирует применение функции griddata.

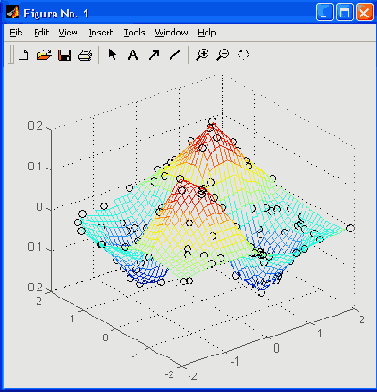
Рис 17.12. Пример использования функции griddata

 

Содержание раздела

---

---