Интерполяция кубическим сплайном

Сплайн-интерполяция используется для представления данных отрезками полиномов невысокой степени — чаще всего третьей. При этом кубическая интерполяция обеспечивает непрерывность первой и второй производных результата интерполяции в узловых точках. Из этого

вытекают следующие свойства кубической сплайн-интерполяции:

график кусочно-полиномиальной аппроксимирующей функции проходит точно через узловые точки;
в узловых точках нет разрывов и резких перегибов функции;
благодаря низкой степени полиномов погрешность между узловыми точками обычно достаточно мала;
связь между числом узловых точек и степенью полинома отсутствует;
поскольку используется множество полиномов, появляется возможность аппроксимации функций с множеством пиков и впадин.

Как отмечалось, в переводе spline означает «гибкая линейка». График интерполирующей функции при этом виде интерполяции можно уподобить кривой, по которой изгибается гибкая линейка, закрепленная в узловых точках. Реализуется сплайн-интерполяция следующей функцией:

yi = spline(x,y,xi) — использует векторы х и у, содержащие аргументы функции и ее значения, и вектор xi, задающий новые точки; для нахождения элементов вектора yi используется кубическая сплайн-интерполяция;
рр = spline(x.y) — возвращает рр-форму сплайна, используемую в функции ppval и других сплайн-функциях.

Пример:

» х=0:10; y=3*cos(x);

» x1=0:0.1:11;

» y1=spline(x,y.x1);

» plot(x,y,'о',x1,y1,'--')

Сплайн-интерполяция дает неплохие результаты для функций, не имеющих разрывов и резких перегибов. Особенно хорошие результаты получаются для монотонных функций.

Результат интерполяции показан на рис. 17.14.

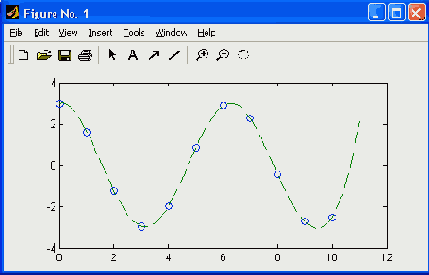
Рис. 17.14. Пример применения функции spline

Ввиду важности сплайн-интерполяции и аппроксимации в обработке и представлении сложных данных в состав системы MATLAB входит пакет расширения Spline Toolbox, содержащий около 70 дополнительных функций, относящихся к реализации сплайн-интерполяции и аппроксимации, а также графического представления сплайнами их результатов. Для вызова данных об этом пакете (если он установлен) используйте команду help splines.

Содержание раздела