Матричная лаборатория MatLab
MATLAB в роли суперкалькулятора
Система MATLAB создана таким образом, что любые (подчас весьма сложные) вычисления можно выполнять в режиме прямых вычислений, то есть без подготовки программы. Это превращает MATLAB в необычайно мощный калькулятор, который способен производить не только обычные для калькуляторов вычисления (например, выполнять арифметические операции и вычислять элементарные функции), но и операции с векторами и матрицами, комплексными числами, рядами и полиномами. Можно почти мгновенно задать и вывести графики различных функций — от простой синусоиды до сложной трехмерной фигуры.
Работа с системой в режиме прямых вычислений носит диалоговый характер и происходит по правилу «задал вопрос, получил ответ». Пользователь набирает на клавиатуре вычисляемое выражение, редактирует его (если нужно) в командной строке и завершает ввод нажатием клавиши ENTER. В качестве примера на рис. 2.9 уже были показаны простейшие вычисления — вычисление выражения 2+3 и значения sin(l).
Даже из таких простых примеров можно сделать некоторые поучительные выводы:
- для указания ввода исходных данных используется символ »;
- данные вводятся с помощью простейшего строчного редактора;
- для блокировки вывода результата вычислений некоторого выражения после него надо установить знак ; (точка с запятой);
- если не указана переменная для значения результата вычислений, то MATLAB назначает такую переменную с именем ans;
- знаком присваивания является привычный математикам знак равенства =, а не комбинированный знак :=, как во многих других языках программирования и математических системах;
- результат вычислений выводится в строках вывода (без знака »);
- встроенные функции (например, sin) записываются строчными буквами, и их аргументы указываются в круглых скобках;
- диалог происходит в стиле «задал вопрос — получил ответ».
Две записи для вектора — V=[l 2 3 4] и V=[1,2,3.4] — являются идентичными. Таким образом, векторы задаются списком своих элементов, разделяемых пробелами или запятыми. Список заключается в квадратные скобки. Для выделения п- го элемента вектора V используется выражение V(n). Оно задает соответствующую индексированную переменную.
В большинстве математических систем вычисление sin(V) и exp(V), где V — вектор, сопровождалось бы выдачей ошибки, поскольку функции sin и ехр должны иметь аргумент в виде скалярной величины. Однако MATLAB — матричная система, а вектор является разновидностью матрицы с размером 1х n. Поэтому в нашем случае результат вычислений будет вектором того же размера, что и аргумент V, но элементы возвращаемого вектора будут синусами или экспонентами от элементов вектора V.
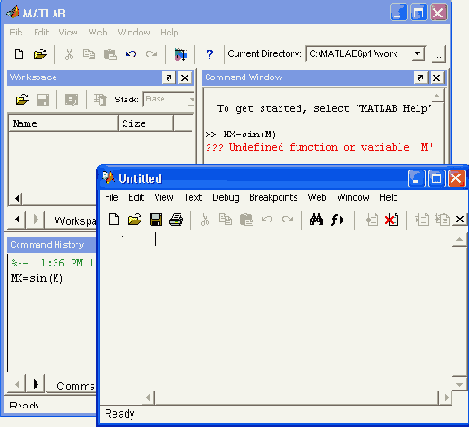
Рис. 2.12. Простейшие операции с матрицей
Еще один пример (рис. 2.12) демонстрирует простейшие операции с матрицей. Здесь задана матрица М с размером 2x2 и вычислена матрица MX=sin(M).
Матрица задается в виде ряда векторов, представляющих ее строки и заключенных в квадратные скобки. Для разделения элементов векторов используется пробелили запятая, а для отделения одного вектора от другого — точка с запятой. Для выделения отдельного элемента матрицы М используется выражение вида M(j,i), где М — имя матрицы, j — номер строки и 1 — номер столбца.
Как видно из приведенных примеров, ввод исходных выражений для вычислений в системе MATLAB осуществляется в самом обычном текстовом формате. В этом же формате выдаются результаты вычислений, за исключением графических. Приведем пример записи вычислений, показанных на рис. 2.8 и 2.9:
То get started, select "MATLAB Help" from the Help menu. » 2+3 ans=
5
» sin(l) ans=
0.8415 » type sin
sin is a built-in function. » help sin SIN Sine.
SIN(X) is the sine'of the elements of X. Overloaded methods
help sym/sin.m
» V=[l 2 3 4] V =
1 2 3 4 » sin(V) ans =
0.8415 0.9093 0.1411 -0.7568 » 3*V ans =
3 6 9 12 » V^2
??? Error using ==> ^ Matrix must be square. » V.^2 ans=
1 4 9 16 » V+2 ans =
3 4 5 6 »
Примечание
Обратите внимание на форму ответов при выполнении простых операций без указания переменной, которой присваивается результат. В таких случаях MATLAB сам назначает переменную ans, которой присваивается результат и значение которой затем выводится на экран.
Сравните эти записи с записями в реальных сессиях (рис. 2.9 и 2.11). Вы наверняка отметите, что они практически идентичны. Разве что в текстовых вариантах примеров для экономии бумаги, на которой печаталась эта книга, убраны пропуски между строками. Мы будем показывать представление сессий в виде прямых копий экрана только в том случае, когда это связано со спецификой проведения вычислений, например когда они сопровождаются выводом графиков или демонстрацией элементов пользовательского интерфейса. В остальных случаях будет использоваться представление сессии прямо в тексте книги в представленном выше текстовом формате — основном для командного режима работы с системой MATLAB. При этом строки ввода будут отмечаться маркером ввода » в их начале. Ради компактности записи пустые строки будут опускаться.