Построение гистограмм

Классическая гистограмма характеризует числа попаданий значений элементов вектора Y в М интервалов с представлением этих чисел в виде столбцовой диаграммы. Для получения данных

для гистограммы служит функция hist, записываемая в следующем виде:

• N=hist(Y) — возвращает вектор чисел попаданий для 10 интервалов, выбираемых автоматически. Если Y — матрица, то выдается массив данных о числе попаданий для каждого из ее столбцов;
• N=hist(Y,M) — аналогична вышерассмотренной, но используется М интервалов (М — скаляр); 
•  N=hist(Y.X) — возвращает числа попаданий элементов вектора Y в интервалы, центры которых заданы элементами вектора X;  
• [N,X]=HIST(...) — возвращает числа попаданий в интервалы и данные о центрах интервалов.

Команда hist(...) с синтаксисом, аналогичным приведенному выше, строит график гистограммы. В следующем примере строится гистограмма для 1000 случайных чисел и выводится вектор с данными о числах их попаданий в интервалы, заданные вектором х:

» х=-3:0.2:3; 

» y=randn(1000,1); 

» hist(y,x)

 » h=hist(y.x) 

h =

Columns 1 through 12

0 0 3 7 8 9 11 23 33 43 57 55

Columns 13 through 24

70 62 83 87 93 68 70 65 41 35 27 21

Columns 25 through 31

12 5 6 3 2 1 0

Построенная гистограмма показана на рис. 6.8.

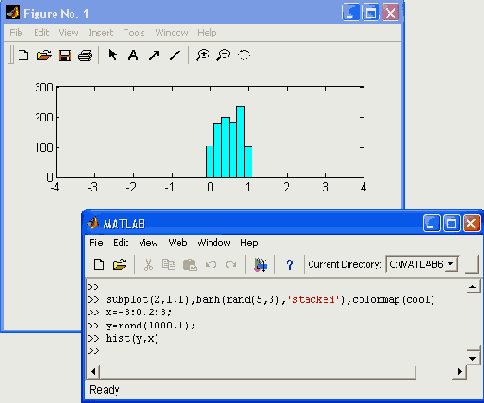
Рис. 6.8. Пример построения гистограммы

Нетрудно заметить, что распределение случайных чисел близко к нормальному закону. Увеличив их количество, можно наблюдать еще большее соответствие этому закону.

 

Содержание раздела

---

---