Тригонометрические и обратные им функции

В системе MATLAB определены следующие тригонометрические и обратные тригонометрические функции. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Напоминаем, что все углы в функциях задаются в радианах.

Э acos (X) — возвращает арккосинус для каждого элемента X. Для действительных значений X в области [-1, 1] acos(X) возвращает действительное значение из диапазона диапазона [0, р], для действительных значений X вне области [-1, 1] acos(X) возвращает комплексное число.

Примеры:

»Y = acos (0.5)

1.0472

» acos([0.5 1 2]) 

ans =

1.0472 0     0 + 1.31701

• acot (X) — возвращает арккотангенс для каждого элемента X. Пример:

» Y=acot(0.l)

у =

1.4711

• acsc(X) — возвращает арккосеканс для каждого элемента X. Пример:
  

» Y= acsc(3)

0.3398

• asec(X) — возвращает арксеканс для каждого элемента X. Пример:

» Y=asec(0.5)

Y =

0 + 1.31701

• asin(X) — возвращает арксинус для каждого элемента X. Для действительных значений X в области [-1, 1] asin(X) возвращает действительное число из диапазона [-р/2, р/2], для действительных значений X вне области [-1, 1] asin(X) возвращает комплексное число. Пример:

» Y= asin (0.278) 

Y =

0.2817

• atan(X) — возвращает арктангенс для каждого элемента X. Для действительных значений X atan(X) находится в области [-р/2, р/2]. Пример:

» Y=atan(1)

Y =

0.7854

• atan2 (Y, X) — возвращает массив Р той же размерности, что X и Y, содержащий поэлементно арктангенсы отношения вещественных частей Y и X. Мнимые части игнорируются. Элементы Р находятся в интервале [-р, р]. Специфический квадрант определен функциями sign(Y) и sign(X). Это отличает полученный результат от результата atan(Y/X), который ограничен интервалом [-л/2, л/2].

Пример:

» atan2(l,2) 

ans = 

0.4636

• cos(X) — возвращает косинус для каждого элемента X. Пример:
  

»Х=[123]; 

» cos(X) 

ans =

0.5403     -0.4161    -0.9900

• cot(X) — возвращает котангенс для каждого элемента X. Пример:

» Y = cot(2) 

Y =

-0.4577

• csc(X) — возвращает косеканс для каждого элемента X. Пример:

» Х=[2 4.678 5:0.987 1 3]; 

» Y = csc(X) 

Y =

1.0998     -1.0006    -1.0428

1.1985     1.1884     7.0862

• sec(X) — возвращает массив той же размерности что и X, состоящий из секансов элементов X. Пример:

» X=[pi/10 pi/3 pi/5]; 

» sec(X) 

ans =

1.0515     2.0000     1.2361

• sin(X) — возвращает синус для каждого элемента X. Пример:

» X=[pi/2 pi/4 pi/6 pi];

» sin(X)

ans =

1.0000     0.7071     0.5000     0.0000

• tan(X) — возвращает тангенс для каждого элемента X.

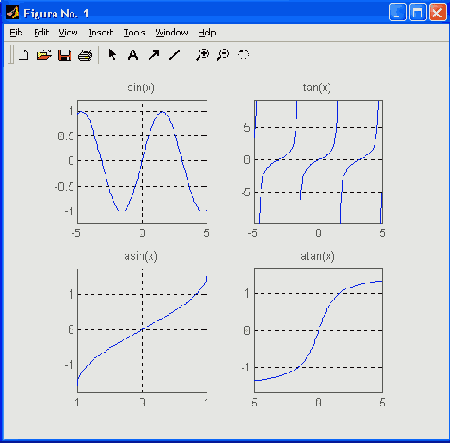
Рис. 8.2. Графики четырех тригонометрических функций

Пример:

» Х=[0.08 0.06 1.09]

X=

0.0800 0.0600 1.0900 

» tan(X)

ans=

0.802     0.0601     1.9171

Следующий файл-сценарий позволяет наблюдать графики четырех тригонометрических функций (рис. 8.2):

syms xsubplot(2.2.1).ezplot(sin(x),[-5 5]).xlabel("),gnd on

subplot(2.2.2),ezp"lot(tan(x).[-5 5]).xlabel(").grid on 

subplot(2,2,3),ezplot(asin(x),[-1 1]).grid on 

subplot(2.2.4),ezplot(atan(x).[-5 5]),grid on

Поскольку многие тригонометрические функции периодичны, появляется возможность формирования из них любопытных комбинаций, позволяющих создавать типовые тестовые сигналы, используемые при моделировании радиоэлектронных устройств. Следующий файл-сценарий строит графики для таких комбинаций, создающих из синусоиды три наиболее распространенных сигнала — прямоугольные, пилообразные и треугольные импульсы:[ В пакете расширения Signal Processing Toolbox есть специальные функции для генерации таких сигналов — square и sawtooth. — Примеч. ред. ]

х=-10:0.01:10;

subplot(2,2.1).plot(x.0.8*sin(x))

.x label('0.8*sin(x)') 

subplot(2.2,2).plot(x,0.8*sign(sin(x)))

.x1abel('0.8*sgn(sin(x))') 

subplot(2.2.3),plot(x.atan(tan(x/2)))

.xlabel('atan(tan(x/2))') 

subplot(2.2.4),plot(x,asin(sin(x)))

.xlabel('asin(sin(x))')

Соответствующие графики представлены на рис. 8.3.

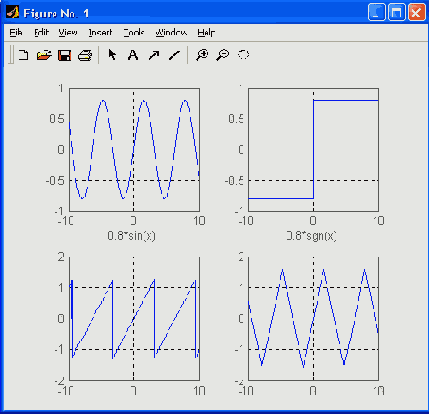
Рис. 8.3. Графики синусоиды, прямоугольных, пилообразных и треугольных колебаний

Дополнительный ряд графиков, полученных комбинациями элементарных функций, показан на рис. 8.4. Эти графики строятся следующим файлом-сценарием:

х=-10:0.01:10;

subplot(2.2.1).plot(x.sin(x). ^A 3).x1abel('sin(xr3')

subplot(2.2.2).plot(x,abs(s1n(x)))

.xlabel('abs(sin(x))').axis([-10 10 -1 1]),

subplot(2.2,3),plot(x,tan(cos(x)))

.xlabel('tanCcos(x))') 

subplot(2.2.4).plot(x.csch(sec(x))),xlabeK'csch(sec(x))')

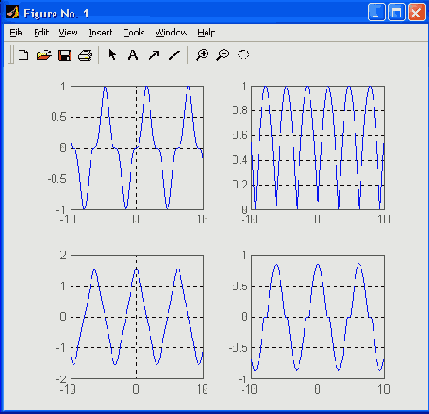
Рис. 8.4. Графики периодических сигналов без разрывов

Эти графики неплохо моделируют сигналы, получаемые при выпрямлении синусоидального напряжения (или тока) и при прохождении синусоидальных сигналов через нелинейные цепи.

 

Содержание раздела

---

---