Ортогональные полиномы Лежандра

Функция Лежандра определяется следующим образом:

где Рn(*) — полином Лежандра степени п, рассчитываемый как

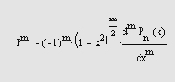
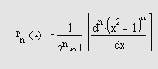
• legendre(n.X) —возвращает функции Лежандра степени п и порядков m = 0,1..... n, вычисленные для элементов X. Аргумент п должен быть скалярным целым числом, не превосходящим 256, а X должен содержать действительные значения в области -UxJl. Возвращаемый массив Р имеет большую размерность, чем X, и каждый элемент P(m+l,dl,d2...) содержит связанную функцию Лежандра степени п и порядка т, вычисленную в точках X(dl,d2...).
• 1egendre(n,X, 'sch') — возвращает квазинормализованные по Шмидту функции Лежандра.

Пример:

» g=rand(3.2);legendre(3,g)

	-0.4469	-0.0277	0.1534
	-0.0558	1.4972	-2.0306
	5.4204	0.2775	4.0079
	-10.5653	-14.9923	-2.7829

ans(:.:.2) =

-0.4472-0.34040.0538

0.0150 -1.0567 -1.9562

5.3514 5.7350 4.4289

-10.7782 -7.3449 -3.4148

 

Содержание раздела

---

---